Spatiotemporal Dynamics of Virus Infection Spreading in Tissues
- PMID: 27997613
- PMCID: PMC5173377
- DOI: 10.1371/journal.pone.0168576
Spatiotemporal Dynamics of Virus Infection Spreading in Tissues
Abstract
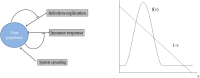
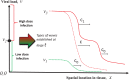
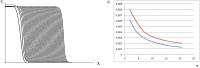
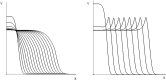
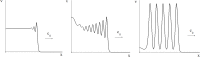
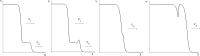
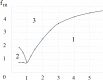
Virus spreading in tissues is determined by virus transport, virus multiplication in host cells and the virus-induced immune response. Cytotoxic T cells remove infected cells with a rate determined by the infection level. The intensity of the immune response has a bell-shaped dependence on the concentration of virus, i.e., it increases at low and decays at high infection levels. A combination of these effects and a time delay in the immune response determine the development of virus infection in tissues like spleen or lymph nodes. The mathematical model described in this work consists of reaction-diffusion equations with a delay. It shows that the different regimes of infection spreading like the establishment of a low level infection, a high level infection or a transition between both are determined by the initial virus load and by the intensity of the immune response. The dynamics of the model solutions include simple and composed waves, and periodic and aperiodic oscillations. The results of analytical and numerical studies of the model provide a systematic basis for a quantitative understanding and interpretation of the determinants of the infection process in target organs and tissues from the image-derived data as well as of the spatiotemporal mechanisms of viral disease pathogenesis, and have direct implications for a biopsy-based medical testing of the chronic infection processes caused by viruses, e.g. HIV, HCV and HBV.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

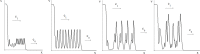
Similar articles
-
Study on the blood-borne virus co-infection and T lymphocyte subset among intravenous drug users.World J Gastroenterol. 2007 Apr 28;13(16):2357-62. doi: 10.3748/wjg.v13.i16.2357. World J Gastroenterol. 2007. PMID: 17511038 Free PMC article.
-
Prevalence of human immunodeficiency virus, hepatitis C virus, hepatitis B virus and syphilis among individuals attending anonymous testing for HIV in Luanda, Angola.S Afr Med J. 2013 Jan 24;103(3):186-8. doi: 10.7196/samj.6097. S Afr Med J. 2013. PMID: 23472697
-
Hepatitis B virus and hepatitis C virus infection among HIV-1-infected injection drug users in Dali, China: prevalence and infection status in a cross-sectional study.Arch Virol. 2015 Apr;160(4):929-36. doi: 10.1007/s00705-014-2311-0. Epub 2015 Jan 24. Arch Virol. 2015. PMID: 25616842
-
Immunology of hepatitis B virus and hepatitis C virus infection.Nat Rev Immunol. 2005 Mar;5(3):215-29. doi: 10.1038/nri1573. Nat Rev Immunol. 2005. PMID: 15738952 Review.
-
Regulatory T cells in viral hepatitis.World J Gastroenterol. 2007 Sep 28;13(36):4858-64. doi: 10.3748/wjg.v13.i36.4858. World J Gastroenterol. 2007. PMID: 17828817 Free PMC article. Review.
Cited by
-
A reaction-diffusion within-host HIV model with cell-to-cell transmission.J Math Biol. 2018 Jun;76(7):1831-1872. doi: 10.1007/s00285-017-1202-x. Epub 2018 Jan 5. J Math Biol. 2018. PMID: 29305736
-
Emergence and competition of virus variants in respiratory viral infections.Front Immunol. 2023 Feb 14;13:945228. doi: 10.3389/fimmu.2022.945228. eCollection 2022. Front Immunol. 2023. PMID: 37168105 Free PMC article.
-
The rate of viral transfer between upper and lower respiratory tracts determines RSV illness duration.J Math Biol. 2019 Jul;79(2):467-483. doi: 10.1007/s00285-019-01364-1. Epub 2019 Apr 22. J Math Biol. 2019. PMID: 31011792
-
A modular framework for multiscale, multicellular, spatiotemporal modeling of acute primary viral infection and immune response in epithelial tissues and its application to drug therapy timing and effectiveness.PLoS Comput Biol. 2020 Dec 21;16(12):e1008451. doi: 10.1371/journal.pcbi.1008451. eCollection 2020 Dec. PLoS Comput Biol. 2020. PMID: 33347439 Free PMC article.
-
A modular framework for multiscale, multicellular, spatiotemporal modeling of acute primary viral infection and immune response in epithelial tissues and its application to drug therapy timing and effectiveness: A multiscale model of viral infection in epithelial tissues.bioRxiv [Preprint]. 2020 Sep 26:2020.04.27.064139. doi: 10.1101/2020.04.27.064139. bioRxiv. 2020. Update in: PLoS Comput Biol. 2020 Dec 21;16(12):e1008451. doi: 10.1371/journal.pcbi.1008451. PMID: 32511367 Free PMC article. Updated. Preprint.
References
-
- Zinkernagel RM, Hengartner H, Stitz L. On the role of viruses in the evolution of immune responses. Br Med Bull. 1985;41(1):92–7. - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

