Measurement of amyloid formation by turbidity assay-seeing through the cloud
- PMID: 28003859
- PMCID: PMC5135725
- DOI: 10.1007/s12551-016-0233-7
Measurement of amyloid formation by turbidity assay-seeing through the cloud
Abstract
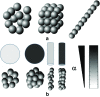
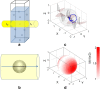
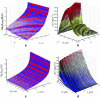
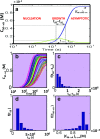
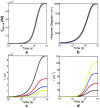
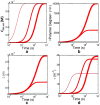
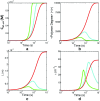
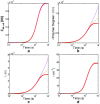
Detection of amyloid growth is commonly carried out by measurement of solution turbidity, a low-cost assay procedure based on the intrinsic light scattering properties of the protein aggregate. Here, we review the biophysical chemistry associated with the turbidimetric assay methodology, exploring the reviewed literature using a series of pedagogical kinetic simulations. In turn, these simulations are used to interrogate the literature concerned with in vitro drug screening and the assessment of amyloid aggregation mechanisms.
Keywords: Amyloid aggregation kinetics; Amyloid biophysics; Data reduction; Nonlinear signal response; Turbidimetric method.
Conflict of interest statement
Compliance with ethical standards Conflict of interests Ran Zhao declares that he has no conflict of interest. Masatomo So declares that he has no conflict of interest. Hendrik Maat declares that he has no conflict of interest. Nicholas J. Ray declares that he has no conflict of interest. Fumio Arisaka declares that he has no conflict of interest. Yuji Goto declares that he has no conflict of interest. John A. Carver declares that he has no conflict of interest. Damien Hall declares that he has no conflict of interest. Ethical approval This article does not contain any studies with human participants or animals performed byany of the authors.
Figures



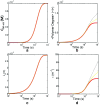
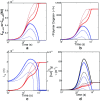
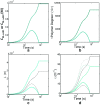
References
-
- Adamcik J, Mezzenga R. Proteins fibrils from a polymer physics perspective. Macromolecules. 2011;45:1137–1150. doi: 10.1021/ma202157h. - DOI
-
- Aldous DJ (1999) Deterministic and stochastic models for coalescence (aggregation and coagulation): a review of the mean-field theory for probabilists. Bernoulli 5:3–48
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

