Fixation Probabilities for Any Configuration of Two Strategies on Regular Graphs
- PMID: 28004806
- PMCID: PMC5177945
- DOI: 10.1038/srep39181
Fixation Probabilities for Any Configuration of Two Strategies on Regular Graphs
Abstract
Population structure and spatial heterogeneity are integral components of evolutionary dynamics, in general, and of evolution of cooperation, in particular. Structure can promote the emergence of cooperation in some populations and suppress it in others. Here, we provide results for weak selection to favor cooperation on regular graphs for any configuration, meaning any arrangement of cooperators and defectors. Our results extend previous work on fixation probabilities of rare mutants. We find that for any configuration cooperation is never favored for birth-death (BD) updating. In contrast, for death-birth (DB) updating, we derive a simple, computationally tractable formula for weak selection to favor cooperation when starting from any configuration containing any number of cooperators. This formula elucidates two important features: (i) the takeover of cooperation can be enhanced by the strategic placement of cooperators and (ii) adding more cooperators to a configuration can sometimes suppress the evolution of cooperation. These findings give a formal account for how selection acts on all transient states that appear in evolutionary trajectories. They also inform the strategic design of initial states in social networks to maximally promote cooperation. We also derive general results that characterize the interaction of any two strategies, not only cooperation and defection.
Figures
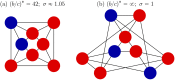
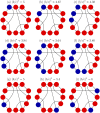
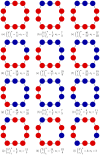
 , which is achieved by just (e) and its conjugate; adding additional cooperators to the configuration in (e) only increases
, which is achieved by just (e) and its conjugate; adding additional cooperators to the configuration in (e) only increases  . The configuration of (e) is ‘optimal’ for cooperation in the sense that if selection increases the fixation probability of cooperators in some state, then it does so in state (e) as well. Relative to all possible initial states, selection can increase the fixation probability of cooperators in (e) under the smallest b/c ratio. Panels (g–i) show that when cooperators are added in a different order (starting with just a single cooperator), the critical benefit-to-cost ratio can actually be increased. Each of these three configurations has isolated cooperators, and (i) gives the global maximum of
. The configuration of (e) is ‘optimal’ for cooperation in the sense that if selection increases the fixation probability of cooperators in some state, then it does so in state (e) as well. Relative to all possible initial states, selection can increase the fixation probability of cooperators in (e) under the smallest b/c ratio. Panels (g–i) show that when cooperators are added in a different order (starting with just a single cooperator), the critical benefit-to-cost ratio can actually be increased. Each of these three configurations has isolated cooperators, and (i) gives the global maximum of  , which is achieved by just (i) and its conjugate. Since N0 = 3, (i) is a maximal isolated configuration. The initial state in (i) is least conducive to cooperation in the sense that, relative to all other initial configurations, (i) requires the largest b/c ratio for selection to increase the fixation probability of cooperators. If selection increases this fixation probability when starting from state (i), then it does so when starting from any other mixed initial configuration.
, which is achieved by just (i) and its conjugate. Since N0 = 3, (i) is a maximal isolated configuration. The initial state in (i) is least conducive to cooperation in the sense that, relative to all other initial configurations, (i) requires the largest b/c ratio for selection to increase the fixation probability of cooperators. If selection increases this fixation probability when starting from state (i), then it does so when starting from any other mixed initial configuration.
Similar articles
-
Fixation properties of multiple cooperator configurations on regular graphs.Theory Biosci. 2019 Nov;138(2):261-275. doi: 10.1007/s12064-019-00293-3. Epub 2019 Mar 21. Theory Biosci. 2019. PMID: 30900107
-
Properties of network structures, structure coefficients, and benefit-to-cost ratios.Biosystems. 2019 Jun;180:88-100. doi: 10.1016/j.biosystems.2019.03.005. Epub 2019 Mar 23. Biosystems. 2019. PMID: 30914346
-
Evolutionary graph theory: breaking the symmetry between interaction and replacement.J Theor Biol. 2007 Jun 21;246(4):681-94. doi: 10.1016/j.jtbi.2007.01.024. Epub 2007 Feb 8. J Theor Biol. 2007. PMID: 17350049 Free PMC article.
-
Evolutionary dynamics under partner preferences.J Theor Biol. 2023 Jan 21;557:111340. doi: 10.1016/j.jtbi.2022.111340. Epub 2022 Nov 5. J Theor Biol. 2023. PMID: 36343667
-
Evolutionary dynamics for persistent cooperation in structured populations.Phys Rev E Stat Nonlin Soft Matter Phys. 2015 Jun;91(6):062802. doi: 10.1103/PhysRevE.91.062802. Epub 2015 Jun 5. Phys Rev E Stat Nonlin Soft Matter Phys. 2015. PMID: 26172749
Cited by
-
A mathematical formalism for natural selection with arbitrary spatial and genetic structure.J Math Biol. 2019 Mar;78(4):1147-1210. doi: 10.1007/s00285-018-1305-z. Epub 2018 Nov 14. J Math Biol. 2019. PMID: 30430219
-
Fixation properties of multiple cooperator configurations on regular graphs.Theory Biosci. 2019 Nov;138(2):261-275. doi: 10.1007/s12064-019-00293-3. Epub 2019 Mar 21. Theory Biosci. 2019. PMID: 30900107
-
Evolution of prosocial behaviours in multilayer populations.Nat Hum Behav. 2022 Mar;6(3):338-348. doi: 10.1038/s41562-021-01241-2. Epub 2022 Jan 3. Nat Hum Behav. 2022. PMID: 34980900
-
Evaluating the structure-coefficient theorem of evolutionary game theory.Proc Natl Acad Sci U S A. 2022 Jul 12;119(28):e2119656119. doi: 10.1073/pnas.2119656119. Epub 2022 Jul 5. Proc Natl Acad Sci U S A. 2022. PMID: 35787041 Free PMC article.
References
-
- Zaggl M. A. Eleven mechanisms for the evolution of cooperation. J. Inst. Econ. 10, 197–230 (2013).
-
- Nowak M. A. Evolutionary Dynamics: Exploring the Equations of Life (Belknap Press, 2006a).
-
- Nowak M. A., Sasaki A., Taylor C. & Fudenberg D. Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650 (2004). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

