Stability in skipping gaits

Abstract

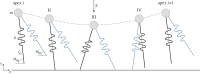
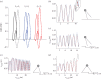
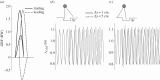
As an alternative to walking and running, humans are able to skip. However, adult humans avoid it. This fact seems to be related to the higher energetic costs associated with skipping. Still, children, some birds, lemurs and lizards use skipping gaits during daily locomotion. We combined experimental data on humans with numerical simulations to test whether stability and robustness motivate this choice. Parameters for modelling were obtained from 10 male subjects. They locomoted using unilateral skipping along a 12 m runway. We used a bipedal spring loaded inverted pendulum to model and to describe the dynamics of skipping. The subjects displayed higher peak ground reaction forces and leg stiffness in the first landing leg (trailing leg) compared to the second landing leg (leading leg). In numerical simulations, we found that skipping is stable across an amazing speed range from skipping on the spot to fast running speeds. Higher leg stiffness in the trailing leg permits longer strides at same system energy. However, this strategy is at the same time less robust to sudden drop perturbations than skipping with a stiffer leading leg. A slightly higher stiffness in the leading leg is most robust, but might be costlier.

Keywords: biomechanics; locomotion; skipping; slip; stability.

Figure 1.

Gait phases during skipping and model parameters. The cycle starts at the highest vertical position (apex). Both legs (black: trailing; grey: leading) are airborne and have different fixed angles with respect to the ground (α_0t, respectively, α_0l). The trailing leg touches the ground first (II). The contact of the leading leg with the ground initiates the double support phase (III). This phase finishes when the trailing leg loses contact (IV). After the leading leg loses contact, the model re-enters the aerial phase. The cycle is completed when the model reaches the apex again. g, gravity; k, leg stiffness; l₀, leg length at TD; m, body mass. Note that for a model having massless legs no difference exists between unilateral and bilateral skipping. The BSLIP model for skipping was first introduced by Minetti [1].

Figure 2.

Fields of stable skipping gaits. To facilitate comparison between species, we present data dimensionless. (a) Leg angles at TD versus dimensionless speed ($\hat{u}=v\text{/}\sqrt{g{l}_0}$). (b) Leg angles at TD versus dimensionless stiffness ($\hat{k}=k{l}_0\text{/}mg$). Leading refers to the leg that is foremost. Trailing leg touches the ground first.

Figure 3.

Influence of leg stiffness asymmetries on (a) profile of GRF, (b) distance travelled and (c–e) robustness against sudden drops. (a) Solid line, trailing leg; dashed line, leading leg. Left, both legs have same stiffness (black), middle, trailing leg 5% higher stiffness (blue); right trailing leg 5% lower stiffness (red). (b–e) Both legs have same stiffness (black), trailing leg 5% higher stiffness (dot blue); trailing leg 5% lower stiffness (dashed-dotted red). (b) Larger distances can be achieved with higher stiffness in the trailing leg. (c,d) For skipping with relatively more protracted leg, as observed in humans, higher stiffness in the leading leg is more robust against perturbations. (e) Skipping gaits that use a more retracted trailing and leading legs are more robust to sudden perturbations. Simulation parameters for (a–d): α_t0 = 75°; α_l0 = 55°; E = 1440 J; y₀ = 1.0389 m; k = 12 000 N m⁻¹. Simulation parameters for (e) α_t0 = 91°; α_l0 = 71°; E = 1300 J; y₀ = 1.0934 m; k = 38 000 N m^−1.

Figure 4.

Skipping with a retracted trailing leg (leg angle > 90°). (a) Even terrain. The trailing leg only accelerates, and the leading leg in most of the cases only decelerates. (b,c) The use of a more retracted trailing leg is more robust against larger perturbations. (b) Trailing leg drop-in perturbation. (c) Leading leg drop-in perturbation. In (b,c), the oscillations of the CoM from two simulations with a step-down step-up perturbation are shown (1 cm, respectively, 5 cm). Note that after the 1 cm perturbation, the model returns to the same fixed point (periodic oscillation). The model can also deal with a 5 cm perturbation; however in this case, the model shifts to a different fixed point. Obviously, for this parameter combination at least two stable limit cycles exist. Simulation parameters: α_t0 = 101°; α_l0 = 57°; E = 940 J; y₀ = 1.0998 m; both legs have same k = 19 000 N m⁻¹.