A continuous ideal free distribution approach to the dynamics of selfish, cooperative and kleptoparasitic populations
- PMID: 28018667
- PMCID: PMC5180165
- DOI: 10.1098/rsos.160788
A continuous ideal free distribution approach to the dynamics of selfish, cooperative and kleptoparasitic populations
Abstract
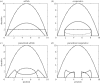
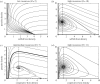
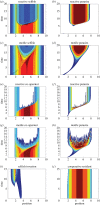
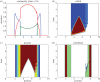
Population distributions depend upon the aggregate behavioural responses of individuals to a range of environmental factors. We extend a model of ideally motivated populations to describe the local and regional consequences of interactions between three populations distinguished by their levels of cooperation and exploitation. Inspired by the classic prisoner's dilemma game, stereotypical fitness functions describe a baseline non-cooperative population whose per capita fitness decreases with density, obligate co-operators who initially benefit from the presence of conspecifics, and kleptoparasites who require heterospecifics to extract resources from the environment. We examine these populations in multiple combinations, determine where both local and regional coexistence is permitted, and investigate conditions under which one population will invade another. When they invade co-operators in resource-rich areas, kleptoparasites initiate a dynamic instability that leads to the loss of both populations; however, selfish hosts, who can persist at low densities, are immune to this risk. Furthermore, adaptive movement may delay the onset of instability as dispersal relieves dynamic stress. Selfish and cooperative populations default to mutual exclusion, but asymmetric variations in interference strength may relax this condition and permit limited sympatry within the environment. Distinct sub-communities characterize the overall spatial structure.
Keywords: cooperation; ideal free movement; interference competition; kleptoparasitism; spatial structure; sympatry.
Figures


Similar articles
-
Bacteria and game theory: the rise and fall of cooperation in spatially heterogeneous environments.Interface Focus. 2014 Aug 6;4(4):20140029. doi: 10.1098/rsfs.2014.0029. Interface Focus. 2014. PMID: 25097750 Free PMC article. Review.
-
Tactical population movements and distributions for ideally motivated competitors.Am Nat. 2010 Nov;176(5):638-50. doi: 10.1086/656494. Am Nat. 2010. PMID: 20887191
-
Dynamic aspiration based on Win-Stay-Lose-Learn rule in spatial prisoner's dilemma game.PLoS One. 2021 Jan 4;16(1):e0244814. doi: 10.1371/journal.pone.0244814. eCollection 2021. PLoS One. 2021. PMID: 33395443 Free PMC article.
-
Survivor's dilemma: The evolution of cooperation in volatile environments.J Theor Biol. 2021 May 7;516:110603. doi: 10.1016/j.jtbi.2021.110603. Epub 2021 Jan 26. J Theor Biol. 2021. PMID: 33508324
-
Variable investment, the Continuous Prisoner's Dilemma, and the origin of cooperation.Proc Biol Sci. 1999 Sep 7;266(1430):1723-8. doi: 10.1098/rspb.1999.0838. Proc Biol Sci. 1999. PMID: 10518320 Free PMC article.
Cited by
-
Evolution and stability of social learning in animal migration.Mov Ecol. 2025 Jun 13;13(1):43. doi: 10.1186/s40462-025-00564-3. Mov Ecol. 2025. PMID: 40514745 Free PMC article.
-
Spatial and temporal patterns of a pulsed resource dynamically drive the distribution of specialist herbivores.Sci Rep. 2019 Nov 28;9(1):17787. doi: 10.1038/s41598-019-54297-6. Sci Rep. 2019. PMID: 31780724 Free PMC article.
-
Dynamical facilitation of the ideal free distribution in nonideal populations.Ecol Evol. 2018 Jan 31;8(5):2471-2481. doi: 10.1002/ece3.3811. eCollection 2018 Mar. Ecol Evol. 2018. PMID: 29531668 Free PMC article.
References
-
- Cressman R, Křivan V, Garay J. 2004. Ideal free distributions, evolutionary games, and population dynamics in multiple-species environments. Am. Nat. 164, 473–489. (doi:10.1086/423827) - DOI - PubMed
-
- Rowell JT. 2009. The limitation of species range: a consequence of searching along resource gradients. Theor. Popul. Biol. 75, 216–227. (doi:10.1016/j.tpb.2009.03.001) - DOI - PMC - PubMed
-
- Rowell JT. 2010. Tactical population movements and distributions for ideally motivated competitors. Am. Nat. 176, 638–650. (doi:10.1086/656494) - DOI - PubMed
-
- Cosner C. 2005. A dynamic model for the ideal-free distribution as a partial differential equation. Theor. Popul. Biol. 67, 101–108. (doi:10.1016/j.tpb.2004.09.002) - DOI - PubMed
-
- Cosner C, Winkler M. 2014. Well-posedness and qualitative properties of a dynamical model for the ideal free distribution. J. Math. Biol. 69, 1343–1382. (doi:10.1007/s00285-013-0733-z) - DOI - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources

