A continuous ideal free distribution approach to the dynamics of selfish, cooperative and kleptoparasitic populations

Abstract

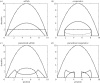
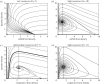
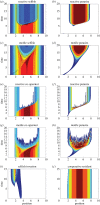
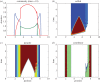
Population distributions depend upon the aggregate behavioural responses of individuals to a range of environmental factors. We extend a model of ideally motivated populations to describe the local and regional consequences of interactions between three populations distinguished by their levels of cooperation and exploitation. Inspired by the classic prisoner's dilemma game, stereotypical fitness functions describe a baseline non-cooperative population whose per capita fitness decreases with density, obligate co-operators who initially benefit from the presence of conspecifics, and kleptoparasites who require heterospecifics to extract resources from the environment. We examine these populations in multiple combinations, determine where both local and regional coexistence is permitted, and investigate conditions under which one population will invade another. When they invade co-operators in resource-rich areas, kleptoparasites initiate a dynamic instability that leads to the loss of both populations; however, selfish hosts, who can persist at low densities, are immune to this risk. Furthermore, adaptive movement may delay the onset of instability as dispersal relieves dynamic stress. Selfish and cooperative populations default to mutual exclusion, but asymmetric variations in interference strength may relax this condition and permit limited sympatry within the environment. Distinct sub-communities characterize the overall spatial structure.

Keywords: cooperation; ideal free movement; interference competition; kleptoparasitism; spatial structure; sympatry.

Figure 1.

Isolated and parasitized hosts. Isolated host populations have long-term distributions (solid grey) that are at dynamic equilibrium and are ideal with uniform fitness (dashed) for a given resource curve (dotted). (a) Selfish population in isolation. (b) Cooperative population in isolation (unstable lower solution also shown). (c) Introduction of kleptoparasites (dashed grey) to selfish hosts results in new ideal distribution at steady state. (d) Parasitism risks destabilizing the central area of cooperative populations with excessive resources. For all panels, host parameters are μ_i=2, r_i=1, a_ij=1, h=1 and α=1.5. Parasitic parameters are μ₃=1, r₃=1 and θ_i=0.205. Sensitivity to fitness is a common value k=0.001. Resources are R(x)=10−0.4(x−5)².

Figure 2.

Parasite–host dynamics. Each panel shows the phase plane of a local (non-spatial) two-population model under different resources. Nullclines (broken lines) are shown for both host (lighter grey) and parasite (darker grey). (a) A marginal value refuge for the selfish host in which the parasite cannot persist. (b) Parasites persist at higher resource levels with selfish population. (c) Parasitism of co-operators divides the phase plane into two basins of attraction for (0,0) and coexistence state (${\tilde{u}}_2,{\tilde{u}}_3$). (d) Parasitism destabilizes the system at high resources, and both populations are lost. All parameters as in figure 1.

Figure 3.

Spatial structure of pairwise interactions. For each pair of species (by row), an invader population is introduced on the left of the inhabited environment at small number. Reactive populations perform local dynamics more quickly than movement with r_i=10, μ₁=μ₂=20 and μ₃=10 while k=0.1. Motile populations have parameters as in figure 1, but k=1. Heat maps: white indicates population density below detection threshold (0.1), while dark red represents 5+/2.5+ densities for hosts/parasites. During response of reactive selfish hosts (a) to spread of reactive parasites (b), displacement is similar to travelling wave. By contrast, motile parasites centralize (d) before expanding outward within the host's range (c). Level curves for parasite density are overlayed atop host heat maps. Reactive co-operators retain marginal and adjacent territories (e) as parasites create a disruption wave that isolates the community (f). In mobile communities (g,h), the disruption only occurs after the parasite is widespread. In host competition under weak interspecific interference (a₁₂=0.2 and a₂₁=0.5), selfish invaders manifest two populated regions that eventually merge (i). The resident co-operators are largely unaffected (j). Resources in (e–j) are R(x)= 11.25−0.5x².

Figure 4.

Local host interactions. Selfish and cooperative populations compete locally under different interference strengths. Nullclines are shown for selfish (light grey) and cooperative populations (dark grey), along with trajectories. (a) Coexistence state is a saddle (a_ij=1). (b) Selfish dominance (a₂₁=1.3, a₁₂=0.1). (c) Mutual exclusion without coexistence (α=2.1, a₁₂=5, a₂₁=0.9). (d) Weak interspecific interference adds a second, stable coexistence state (a₁₂=0.1, a₂₁=0.3).

Figure 5.

Community evolution: different trajectories for the three-species community dynamics are shown when the hosts remain mutually exclusive. (a) θ_i= 0.15, two local host–parasite attractors. (b) Co-operators persist against parasites, but are weakened sufficiently for selfish hosts to invade (θ_i=0.20). (c) Co-operators are destabilized in the face of parasitism (θ_i=0.30). (d) In-depth look at local behaviour of co-operator–parasite equilibrium where host is weakened but not yet vulnerable to invasion by selfish hosts (θ_i=0.19). In all plots, resources are set to R=10, while all other parameters equal 1.

Figure 6.

Sequential introductions. A small selfish population is introduced to the community already containing co-operative and exploitative populations. (a) Community composition at end of simulation is almost ideal but not symmetric. Red, parasite; blue, co-operator; green, selfish. (b) Selfish invaders move rapidly across the uninhabited interior. (c) Parasites trail selfish hosts at reduced speed. (d) Co-ooperators on left are mostly unaffected by the community change. Those on the right are disrupted upon contact with the selfish expansion front. All parameters as in figure 3 for reactive populations, and R(x)=11.25−0.5x².