Micromechanics of sea ice frictional slip from test basin scale experiments
- PMID: 28025302
- PMCID: PMC5179962
- DOI: 10.1098/rsta.2015.0354
Micromechanics of sea ice frictional slip from test basin scale experiments
Abstract
We have conducted a series of high-resolution friction experiments on large floating saline ice floes in an environmental test basin. In these experiments, a central ice floe was pushed between two other floes, sliding along two interfacial faults. The frictional motion was predominantly stick-slip. Shear stresses, normal stresses, local strains and slip displacement were measured along the sliding faults, and acoustic emissions were monitored. High-resolution measurements during a single stick-slip cycle at several positions along the fault allowed us to identify two phases of frictional slip: a nucleation phase, where a nucleation zone begins to slip before the rest of the fault, and a propagation phase when the entire fault is slipping. This is slip-weakening behaviour. We have therefore characterized what we consider to be a key deformation mechanism in Arctic Ocean dynamics. In order to understand the micromechanics of sea ice friction, we have employed a theoretical constitutive relation (i.e. an equation for shear stress in terms of temperature, normal load, acceleration, velocity and slip displacement) derived from the physics of asperity-asperity contact and sliding (Hatton et al. 2009 Phil. Mag. 89, 2771-2799 (doi:10.1080/14786430903113769)). We find that our experimental data conform reasonably with this frictional law once slip weakening is introduced. We find that the constitutive relation follows Archard's law rather than Amontons' law, with [Formula: see text] (where τ is the shear stress and σn is the normal stress) and n = 26/27, with a fractal asperity distribution, where the frictional shear stress, τ = ffractal Tmlws, where ffractal is the fractal asperity height distribution, Tml is the shear strength for frictional melting and lubrication and ws is the slip weakening. We can therefore deduce that the interfacial faults failed in shear for these experimental conditions through processes of brittle failure of asperities in shear, and, at higher velocities, through frictional heating, localized surface melting and hydrodynamic lubrication.This article is part of the themed issue 'Microdynamics of ice'.
Keywords: micromechanics; scaling; sea ice friction.
© 2016 The Author(s).
Figures



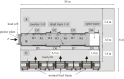


 of the central ice sheet, and the acceleration
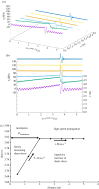
of the central ice sheet, and the acceleration  of the central ice sheet, during a single stick–slip event in experiment 1–4, are plotted, as points; the subscripts ‘4’ and ‘2’ index the positions along the fault where the shear stress sensor and displacement were measured; these are roughly equivalent positions (figure 4). D2start-1 is an arbitrary origin for displacement. (a) Shear stress is plotted against displacement. (b) Shear stress is plotted against velocity. (c) Velocity is plotted against displacement. (d) Acceleration is plotted against displacement. (e) Shear stress is plotted against acceleration.
of the central ice sheet, during a single stick–slip event in experiment 1–4, are plotted, as points; the subscripts ‘4’ and ‘2’ index the positions along the fault where the shear stress sensor and displacement were measured; these are roughly equivalent positions (figure 4). D2start-1 is an arbitrary origin for displacement. (a) Shear stress is plotted against displacement. (b) Shear stress is plotted against velocity. (c) Velocity is plotted against displacement. (d) Acceleration is plotted against displacement. (e) Shear stress is plotted against acceleration.



References
-
- Scourfield S, Sammonds P, Lishman L, Marchenko M. 2015. The effect of ice rubble on ice–ice sliding. In Proc 23rd Int. Conf. Port and Ocean Engineering Under Arctic Conditions, Trondheim, Norway, 14–18 June 2015.
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

