A Rough Set Bounded Spatially Constrained Asymmetric Gaussian Mixture Model for Image Segmentation

Abstract

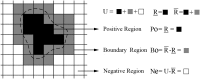
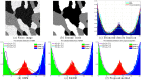
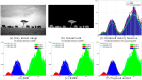
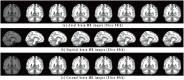
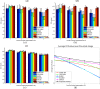
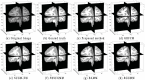
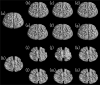
Accurate image segmentation is an important issue in image processing, where Gaussian mixture models play an important part and have been proven effective. However, most Gaussian mixture model (GMM) based methods suffer from one or more limitations, such as limited noise robustness, over-smoothness for segmentations, and lack of flexibility to fit data. In order to address these issues, in this paper, we propose a rough set bounded asymmetric Gaussian mixture model with spatial constraint for image segmentation. First, based on our previous work where each cluster is characterized by three automatically determined rough-fuzzy regions, we partition the target image into three rough regions with two adaptively computed thresholds. Second, a new bounded indicator function is proposed to determine the bounded support regions of the observed data. The bounded indicator and posterior probability of a pixel that belongs to each sub-region is estimated with respect to the rough region where the pixel lies. Third, to further reduce over-smoothness for segmentations, two novel prior factors are proposed that incorporate the spatial information among neighborhood pixels, which are constructed based on the prior and posterior probabilities of the within- and between-clusters, and considers the spatial direction. We compare our algorithm to state-of-the-art segmentation approaches in both synthetic and real images to demonstrate the superior performance of the proposed algorithm.

Fig 1. Illustration of three rough regions.

Fig 2. An example of spatial filters that considers four directions.

From left to right: horizontal, vertical and two diagonal directions.

Fig 3. Examples of testing images.

From left to right: synthetic image, simulated T1-weighted brain MR, real T1-weighted brain MR and natural images.

Fig 4. Illustrations of proposed algorithm.

Fig 5. Illustrations of estimated distributions on synthetic image.

Fig 6. Illustrations of estimated distributions on natural image.

Fig 7. Experimental results on synthetic image with Gaussian noise (image size: 128 × 128).

(a) Original image, (b) Noisy image with Gaussian noise (0 mean, 0.07 variance); segmentation results by applying (c) proposed algorithm (CCR = 0.9954), (d) SCGM-EM (CCR = 0.9942), (e) FRSCGMM (CCR = 0.9906), (f) BAMM (CCR = 0.9131), (g) BGGMM (CCR = 0.9152).

Fig 8. Experimental results on synthetic image with speckle noise (image size: 128 × 128).

(a) Original image, (b) Noisy image with speckle noise (0 mean, 0.04 variance), segmentation results by applying (c) proposed algorithm (CCR = 0.9956), (d) SCGM-EM (CCR = 0.9802), (e) FRSCGMM (CCR = 0.9835), (f) BAMM (CCR = 0.8174), (g) BGGMM (CCR = 0.7456).

Fig 9. Illustration of three simulated T1-weighted brain MR images with 9% noise and corresponding segmentation results obtained by each algorithm.

In each subfigure, the images from left to right show: original image, segmentation results obtained by SCGM-EM, FRSCGMM, BAMM, BGGMM, GRFCM, proposed algorithm, and ground truth.

Fig 10

DC values for: (a) GM segmentation, (b) WM segmentation, (c) CSF segmentation, (d) CCR values over the entire images obtained by applying six segmentation algorithms to simulated brain MR images with increasing noise levels.

Fig 11. 3D slice view of the real dataset (IBSR04), corresponding ground truth and segmentations by applying the proposed method, GRFCM, SCGM-EM, FRSCGMM, BAMM, and BGGMM.

Fig 12. Example of tissue surfaces for case IBSR12.

(a) and (h) show ground truth of GM and WM surfaces, respectively. (b) to (g) show GM surface obtained by SCGM-EM, FRSCGMM, BAMM, BGGMM, GRFCM, and the proposed method, respectively. (i) to (n) show the WM surface obtained by SCGM-EM, FRSCGMM, BAMM, BGGMM, GRFCM, and the proposed method, respectively.

Fig 13. Performance of six segmentation algorithms on 18 benchmark data sets.

Fig 14. Comparison of color image segmentations.

The image IDs are: (a) 105019, (b) 100007, (c) 28083. Images from second to sixth row show segmentation results obtained by SCGM-EM, FRSCGMM, BAMM, BGGMM, and proposed algorithm.