Orbital angular momentum of photons and the entanglement of Laguerre-Gaussian modes

Abstract

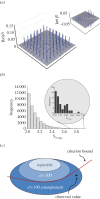
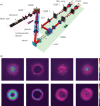
The identification of orbital angular momentum (OAM) as a fundamental property of a beam of light nearly 25 years ago has led to an extensive body of research around this topic. The possibility that single photons can carry OAM has made this degree of freedom an ideal candidate for the investigation of complex quantum phenomena and their applications. Research in this direction has ranged from experiments on complex forms of quantum entanglement to the interaction between light and quantum states of matter. Furthermore, the use of OAM in quantum information has generated a lot of excitement, as it allows for encoding large amounts of information on a single photon. Here, we explain the intuition that led to the first quantum experiment with OAM 15 years ago. We continue by reviewing some key experiments investigating fundamental questions on photonic OAM and the first steps to applying these properties in novel quantum protocols. At the end, we identify several interesting open questions that could form the subject of future investigations with OAM.This article is part of the themed issue 'Optical orbital angular momentum'.

Keywords: Laguerre–Gaussian modes; high-dimensional Hilbert space; orbital angular momentum; photonic quantum experiments.

Figure 1.

(a) The experimental configuration of Mair et al. [3] consisted of an SPDC crystal (BBO), which produced photon pairs entangled in OAM. The entanglement was confirmed by using absorption grating holograms, which transform the OAM value of the mode. Using a single-mode fibre, only Gauss photons were detected, which allowed the OAM value of single photons to be determined (adapted from [3]). (b) Picture of the absorptive hologram used in the Mair experiment (adapted from [4]). (c) The incoherent mixture of a ℓ = 0 and ℓ = 1 mode (which is separable), while (d) shows coherent superpositions between those modes (adapted from [4]). This property can be used to verify entanglement, by measuring the intensity of one photon along the red dotted line, when its partner photon is projected into a superposition of ℓ = 0 and ℓ = 1. (Online version in colour.)

Figure 2.

Three different methods to investigate high-dimensional entanglement. (a) Quantum state tomography, (b) violation of high-dimensional Bell inequalities, (c) entanglement dimensionality witnesses. (a) Quantum tomography, while experimentally and computationally expensive, gives the maximal possible information about the quantum state. The highest-dimensional two-photon state for which quantum tomography (without assumption of state properties) was reported is an eight-dimensionally entangled state. The figure shows the reconstructed density matrix (adapted from [24]). (b) Generalized Bell inequalities can also be used to verify high-dimensional entanglement. These values from [27] show the violation of a three-dimensional Bell inequality by exceeding the classical bound of S₃ = 2 for various settings in the experiment. (c) An entanglement dimensionality (Schmidt Number) witness gives a set of measurements and bounds that a state with entanglement dimension d can maximally reach. If an experiment exceeds this bound, the state was at least (d + 1)-dimensionally entangled. In this image, a situation is depicted where a measurement leads to an observed value exceeding the bound for d = 100-dimensional entanglement (adapted from [28]). (Online version in colour.)

Figure 3.

The ability to measure the OAM of a single photon is very important for quantum experiments. (a) The idea of a non-destructive measurement of the parity of OAM in an interferometric way introduced in [72]. Owing to an OAM-dependent phase introduced by a Dove prism, even and odd modes exit from different output ports. This process can be cascaded for measuring arbitrarily large OAM spectra (adapted from [72]). (b) A refractive method for efficiently separating the OAM eigenstates of a single photon. A log-polar transformation is used to convert the helical phase profile of an OAM mode into a linear phase ramp with an OAM-dependent tilt. Such modes can then be spatially separated via a simple Fourier-transforming lens (adapted from [73]). (Online version in colour.)

Figure 4.

(a) A high-dimensional BB84 QKD experiment has been implemented in [80]. It uses a digital micro-mirror device (DMD) for very fast encoding of spatial modes, and multi-outcome measurements in two mutual unbiased bases (OAM and angular modes) (adapted from [80]). (b) The self-healing character of Bessel modes, which might be useful for long-distance entanglement experiments and QKD. The upper row shows Bessel modes (with non-zero OAM), and the lower one Laguerre–Gauss modes. The second and third images show the beam after an obstruction and after 2 cm of propagation. Interestingly, in the last image after 5 cm of propagation, the Bessel mode reappears while the Laguerre–Gauss mode has not resumed its original structure. The self-healing property has been demonstrated for entanglement in [93] (adapted from [93]). (Online version in colour.)

Figure 5.

Long-distance quantum communication can be done in two different ways. (a) An experiment which distributes OAM entanglement via a photonic crystal fibre [96], with subsequent measurement of a Bell inequality using sector plates. While the fibre was only 30 cm long, the experiment clearly shows that entanglement can in principle be coupled into and transported via fibres (adapted from [96]). An alternative method is the free-space transmission of OAM modes. A 3 km turbulent intra-city link has been shown to support the distribution of entanglement encoded in the first two higher-order modes [97]. In this experiment, a polarization-entangled pair of photons was created, where one of the photons was measured in polarization. The polarization information of the second photon was transferred to OAM and transmitted over 3 km, and measured using the infront of a telescope (adapted from [97]). (Online version in colour.)

Figure 6.

Quantum memories for spatial modes. (a) A quantum memory for high-dimensional entangled states spatially separated by 1 m [109]. On the left side, one sees the energy-level diagram of ⁸⁵Rb, as well as the time sequence for creating and storing entanglement in it. On the right is a sketch of the experimental set-up with two distant magneto-optical traps (MOTs) between which entanglement is generated (adapted from [109]). (b) A quantum memory which can store both the polarization as well as the spatial-mode information of photons is shown. The photons are stored in a cloud of caesium atoms, and the storage time is roughly 1 µs (adapted from [110]). (Online version in colour.)

Figure 7.

Multi-photon quantum experiments involving OAM. In (a), an experiment is shown where two properties of a photon (the polarization and the parity of an ℓ = ±1 spatial mode) are teleported simultaneously. It is possible by a quantum non-demolition measurement, which curiously is implemented itself as a quantum teleportation scheme. For this, six photons are required to teleport the (2 × 2)-dimensional quantum state (adapted from [118]). In (b), an experiment is shown which creates a genuine multi-partite high-dimensional entangled state. Similarly to multi-photon polarization experiments, the which-crystal information is erased by an interferometer that sorts even and odd OAM modes. The resulting state has an asymmetric entanglement structure—a feature that can only exist when both the number of particles and the number of dimensions are larger than 2 (adapted from [75]). (Online version in colour.)