Interpretation of the Precision Matrix and Its Application in Estimating Sparse Brain Connectivity during Sleep Spindles from Human Electrocorticography Recordings
- PMID: 28095202
- PMCID: PMC5424817
- DOI: 10.1162/NECO_a_00936
Interpretation of the Precision Matrix and Its Application in Estimating Sparse Brain Connectivity during Sleep Spindles from Human Electrocorticography Recordings
Abstract
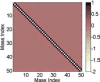
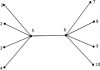
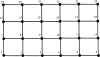
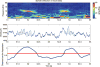
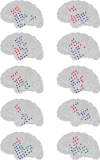
The correlation method from brain imaging has been used to estimate functional connectivity in the human brain. However, brain regions might show very high correlation even when the two regions are not directly connected due to the strong interaction of the two regions with common input from a third region. One previously proposed solution to this problem is to use a sparse regularized inverse covariance matrix or precision matrix (SRPM) assuming that the connectivity structure is sparse. This method yields partial correlations to measure strong direct interactions between pairs of regions while simultaneously removing the influence of the rest of the regions, thus identifying regions that are conditionally independent. To test our methods, we first demonstrated conditions under which the SRPM method could indeed find the true physical connection between a pair of nodes for a spring-mass example and an RC circuit example. The recovery of the connectivity structure using the SRPM method can be explained by energy models using the Boltzmann distribution. We then demonstrated the application of the SRPM method for estimating brain connectivity during stage 2 sleep spindles from human electrocorticography (ECoG) recordings using an [Formula: see text] electrode array. The ECoG recordings that we analyzed were from a 32-year-old male patient with long-standing pharmaco-resistant left temporal lobe complex partial epilepsy. Sleep spindles were automatically detected using delay differential analysis and then analyzed with SRPM and the Louvain method for community detection. We found spatially localized brain networks within and between neighboring cortical areas during spindles, in contrast to the case when sleep spindles were not present.
Figures
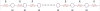

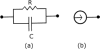






References
-
- Anand A, Li Y, Wang Y, Wu J, Gao S, Bukhari L, Lowe MJ. Antidepressant effect on connectivity of the mood-regulating circuit: An FMRI study. Neuropsychopharmacology. 2005;30(7):1334–1344. - PubMed
-
- Banerjee O, El Ghaoui L, d’Aspremont A. Model selection through sparse maximum likelihood estimation for multivariate gaussian or binary data. Journal of Machine Learning Research. 2008;9:485–516.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

