Spectral consensus strategy for accurate reconstruction of large biological networks

Abstract

Background: The last decades witnessed an explosion of large-scale biological datasets whose analyses require the continuous development of innovative algorithms. Many of these high-dimensional datasets are related to large biological networks with few or no experimentally proven interactions. A striking example lies in the recent gut bacterial studies that provided researchers with a plethora of information sources. Despite a deeper knowledge of microbiome composition, inferring bacterial interactions remains a critical step that encounters significant issues, due in particular to high-dimensional settings, unknown gut bacterial taxa and unavoidable noise in sparse datasets. Such data type make any a priori choice of a learning method particularly difficult and urge the need for the development of new scalable approaches.

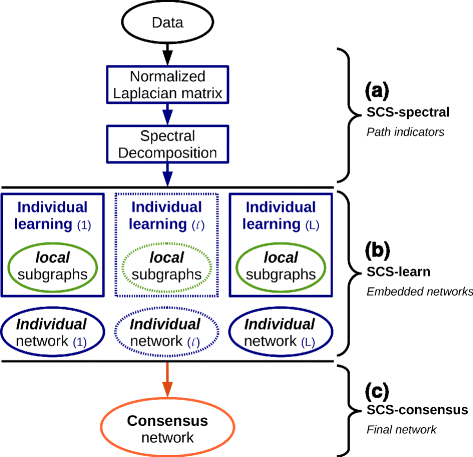
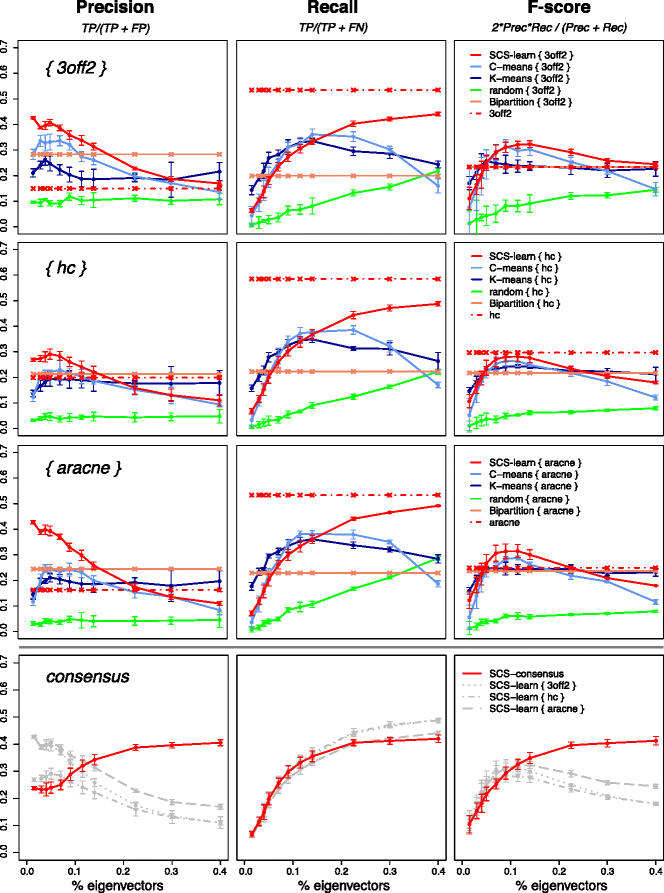
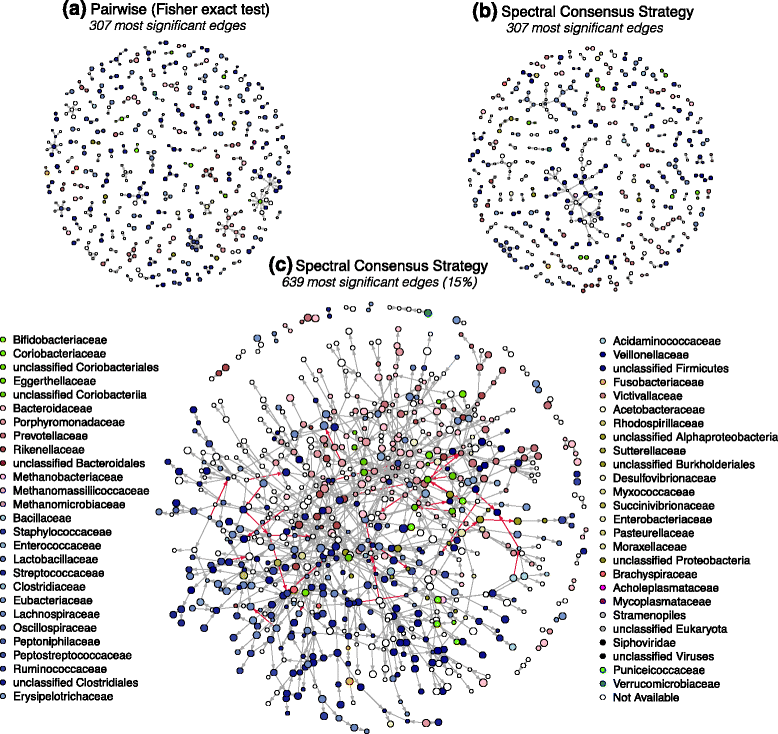
Results: We propose a consensus method based on spectral decomposition, named Spectral Consensus Strategy, to reconstruct large networks from high-dimensional datasets. This novel unsupervised approach can be applied to a broad range of biological networks and the associated spectral framework provides scalability to diverse reconstruction methods. The results obtained on benchmark datasets demonstrate the interest of our approach for high-dimensional cases. As a suitable example, we considered the human gut microbiome co-presence network. For this application, our method successfully retrieves biologically relevant relationships and gives new insights into the topology of this complex ecosystem.

Conclusions: The Spectral Consensus Strategy improves prediction precision and allows scalability of various reconstruction methods to large networks. The integration of multiple reconstruction algorithms turns our approach into a robust learning method. All together, this strategy increases the confidence of predicted interactions from high-dimensional datasets without demanding computations.

Keywords: Community-based method; High-dimensional data; Microbiota; Network reconstruction; Spectral theory.

Fig. 1

Overview of the Spectral Consensus Strategy (SCS). The SCS method unfolds in three parts. a The SCS-spectral phase identifies sets of path-related variables based on the magnitude of the graph Laplacian eigenvector elements. b The SCS-learn phase performs multiple parallel local reconstructions using different learning methods. c The SCS-consensus phase provides a consensus network built on the individual outcomes from the SCS-learn step

Fig. 2

SCS-learn and SCS-consensus evaluations for ANDES benchmark network [223 nodes, 338 edges, 〈k〉=3.03]. Precision, Recall and F-score results for an increasing proportion of eigenvectors (up to 40 %), subgraphs of 12 nodes (5 % variables) and 150 samples. Scores take misorientations into account. Each point is an average over 5 datasets (results for different subgraph and dataset sizes follow a similar trend, see Additional file 1). (SCS-learn, top three rows) Three learning algorithms are embedded to reconstruct a network from subgraphs whose vertices are selected from the magnitude of eigenvector elements (SCS-learn, red solid line), spectral fuzzy C-means partitioning (light blue solid line), spectral K-means clustering (dark blue solid line), random subsets (green solid line) and recursive bi-partitioning (salmon solid line). Results are compared to scores obtained without spectral or partitioning embedding (red dashed line). (SCS-consensus, bottom row) The SCS-learn reconstructions are combined in a consensus network (red solid line) and compared with individual SCS-learn outcomes (gray dashed lines). Scores are computed from the top 338 consensus edges (results for different number of consensus edges follow a similar trend, see Additional file 1)

Fig. 3

Microbial co-presence ecosystem. Microbial ecosystem reconstructed with the pairwise Fisher’s exact test [47] (a) and the SCS approach (b,c). Data for 2, 101 co-abundant groups (CAGs) and n=663 patients recruited in the MetaHIT project were used. Edges depict co-presence (gray edges) or absence-presence (red edges) relationships. a Gut microbial ecosystem based on Fisher’s exact test between pairs of CAGs [47] (307 edges between 445 CAGs of at least 50 genes). b The same number of top-ranked edges (307) obtained with the SCS approach which involve 443 CAGs of at least 50 genes. c The 15 % most significant edges obtained with the SCS approach (654 nodes and 639 edges)

Fig. 4

Edge rank correlations between SCS-learn and SCS-consensus outcomes for human gut microbial ecosystem. 6, 389 edges were predicted from a dataset of 663 observations and 2, 101 CAGs (MetaHIT project [47]). Rank of edges predicted by only one embedded learning method are given in blue (ARACNE, 159 edges), red (3off2, 498 edges) and yellow (hill-climbing, 2, 889 edges). Rank of edges predicted by two individual learning methods are given in green (ARACNE & hill-climbing, 31), orange (3off2 & hill-climbing, 573 edges) and purple (3off2 & ARACNE, 720 edges). Rank of edges predicted by all individual methods are given in black (1, 519 edges)