Control of Movement Initiation Underlies the Development of Balance
- PMID: 28111151
- PMCID: PMC5421408
- DOI: 10.1016/j.cub.2016.12.003
Control of Movement Initiation Underlies the Development of Balance
Abstract
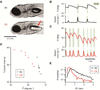
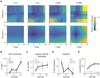
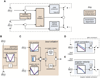
Balance arises from the interplay of external forces acting on the body and internally generated movements. Many animal bodies are inherently unstable, necessitating corrective locomotion to maintain stability. Understanding how developing animals come to balance remains a challenge. Here we study the interplay among environment, sensation, and action as balance develops in larval zebrafish. We first model the physical forces that challenge underwater balance and experimentally confirm that larvae are subject to constant destabilization. Larvae propel in swim bouts that, we find, tend to stabilize the body. We confirm the relationship between locomotion and balance by changing larval body composition, exacerbating instability and eliciting more frequent swimming. Intriguingly, developing zebrafish come to control the initiation of locomotion, swimming preferentially when unstable, thus restoring preferred postures. To test the sufficiency of locomotor-driven stabilization and the developing control of movement timing, we incorporate both into a generative model of swimming. Simulated larvae recapitulate observed postures and movement timing across early development, but only when locomotor-driven stabilization and control of movement initiation are both utilized. We conclude the ability to move when unstable is the key developmental improvement to balance in larval zebrafish. Our work informs how emerging sensorimotor ability comes to impact how and why animals move when they do.
Keywords: control; freely moving; growth; locomotion; morphology; pitch; sensorimotor; swimming; vestibular; zebrafish.
Copyright © 2017 The Authors. Published by Elsevier Ltd.. All rights reserved.
Figures




Comment in
-
Postural Control: Learning to Balance Is a Question of Timing.Curr Biol. 2017 Feb 6;27(3):R105-R107. doi: 10.1016/j.cub.2016.12.021. Curr Biol. 2017. PMID: 28171753
Similar articles
-
The Vestibulospinal Nucleus Is a Locus of Balance Development.J Neurosci. 2024 Jul 24;44(30):e2315232024. doi: 10.1523/JNEUROSCI.2315-23.2024. J Neurosci. 2024. PMID: 38777599 Free PMC article.
-
Movement and function of the pectoral fins of the larval zebrafish (Danio rerio) during slow swimming.J Exp Biol. 2011 Sep 15;214(Pt 18):3111-23. doi: 10.1242/jeb.057497. J Exp Biol. 2011. PMID: 21865524
-
Development of vestibular behaviors in zebrafish.Curr Opin Neurobiol. 2018 Dec;53:83-89. doi: 10.1016/j.conb.2018.06.004. Epub 2018 Jun 26. Curr Opin Neurobiol. 2018. PMID: 29957408 Free PMC article. Review.
-
Cerebellar Purkinje cells control posture in larval zebrafish (Danio rerio).Elife. 2025 Apr 24;13:RP97614. doi: 10.7554/eLife.97614. Elife. 2025. PMID: 40272244 Free PMC article.
-
Principles Governing Locomotion in Vertebrates: Lessons From Zebrafish.Front Neural Circuits. 2018 Sep 13;12:73. doi: 10.3389/fncir.2018.00073. eCollection 2018. Front Neural Circuits. 2018. PMID: 30271327 Free PMC article. Review.
Cited by
-
Optic flow in the natural habitats of zebrafish supports spatial biases in visual self-motion estimation.Curr Biol. 2022 Dec 5;32(23):5008-5021.e8. doi: 10.1016/j.cub.2022.10.009. Epub 2022 Nov 2. Curr Biol. 2022. PMID: 36327979 Free PMC article.
-
Whole-Brain Calcium Imaging during Physiological Vestibular Stimulation in Larval Zebrafish.Curr Biol. 2018 Dec 3;28(23):3723-3735.e6. doi: 10.1016/j.cub.2018.10.017. Epub 2018 Nov 15. Curr Biol. 2018. PMID: 30449666 Free PMC article.
-
A primal role for the vestibular sense in the development of coordinated locomotion.Elife. 2019 Oct 8;8:e45839. doi: 10.7554/eLife.45839. Elife. 2019. PMID: 31591962 Free PMC article.
-
A sensation for inflation: initial swim bladder inflation in larval zebrafish is mediated by the mechanosensory lateral line.bioRxiv [Preprint]. 2023 Apr 24:2023.01.12.523756. doi: 10.1101/2023.01.12.523756. bioRxiv. 2023. PMID: 36712117 Free PMC article. Preprint.
-
Organization of vestibular circuits for postural control in zebrafish.Curr Opin Neurobiol. 2023 Oct;82:102776. doi: 10.1016/j.conb.2023.102776. Epub 2023 Aug 25. Curr Opin Neurobiol. 2023. PMID: 37634321 Free PMC article. Review.
References
-
- Dickinson MH. How animals move: An integrative view. Science. 2000;288:100–106. - PubMed
-
- Aleyev YG. Nekton. First. Springer; 1977.
-
- Webb PW, Weihs D. Stability versus maneuvering: Challenges for stability during swimming by fishes. Integrative and Comparative Biology. 2015;55:753–764. - PubMed
-
- Alexander RM. Functional Design in Fishes. First. Hutchinson University Library; 1967.
-
- Bernstein NA. The coordination and regulation of movements. First. Pergamon; 1967.
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

