Morphological Transformation and Force Generation of Active Cytoskeletal Networks

Abstract

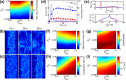
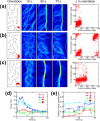
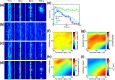
Cells assemble numerous types of actomyosin bundles that generate contractile forces for biological processes, such as cytokinesis and cell migration. One example of contractile bundles is a transverse arc that forms via actomyosin-driven condensation of actin filaments in the lamellipodia of migrating cells and exerts significant forces on the surrounding environments. Structural reorganization of a network into a bundle facilitated by actomyosin contractility is a physiologically relevant and biophysically interesting process. Nevertheless, it remains elusive how actin filaments are reoriented, buckled, and bundled as well as undergo tension buildup during the structural reorganization. In this study, using an agent-based computational model, we demonstrated how the interplay between the density of myosin motors and cross-linking proteins and the rigidity, initial orientation, and turnover of actin filaments regulates the morphological transformation of a cross-linked actomyosin network into a bundle and the buildup of tension occurring during the transformation.

Fig 1. An agent-based computational model was employed for studying bundle formation.

(a) Actin filaments, motors, and actin cross-linking proteins (ACPs) are simplified into cylindrical segments connected by elastic hinges. Actin filaments (blue) are modeled as a series of cylindrical segments with polarity (barbed and pointed ends). Motors (red) consist of a backbone with symmetric polarity and with arms representing myosin motor heads. ACPs (yellow) are modeled as two parallel arms. Arms of motors and ACPs can bind to actin filaments. Equilibrium lengths of segments of actin filaments (A), motors (M), and ACPs are maintained by extensional stiffness (κ_s), whereas equilibrium angles between segments are maintained by bending stiffness (κ_b). (b) An example of bundle formation via compaction of a network. The network (4×8×0.5 μm) consists of actin (teal) with concentration C_A = 40 μM, motor (red) with density R_M = 0.08, and ACP (yellow) with density R_ACP = 0.02. A periodic boundary condition is applied only in the y-direction. After motors start walking at t = 0 s, initially homogeneous network compacts into a bundle within 20 s.

Fig 2. Densities of motors (R_M) and ACPs (R_ACP) determine characteristics of bundle formation and tension generation.

(a-b) Snapshots showing actin density for (a) unsuccessful (R_M = 0.08, R_ACP = 0.01) and (b) successful bundle formation (R_M = 0.08, R_ACP = 0.1). (a) At t = 10 s, the bundle has heterogeneous actin distribution with dangling actin filaments. The bundle further aggregates into a few clumps over time (t = 30 s and 60 s). (b) The bundle has relatively homogeneous actin distribution at t = 10 s and remains stable during and after compaction (t = 30 s and 60 s). (c) Time evolution of tensile forces generated by bundles shown in (a) and (b). The case with unsuccessful bundle formation (red circle) shows lower tension which decreases faster than tension in the case with successful bundle formation (blue triangle). (d) Distribution of forces exerted on motors ($f_{\mathrm{M}}^{\max }$) and ACPs ($f_{\mathrm{ACP}}^{\max }$) measured at peak tension for cases shown in (a) and (b). The gray dashed line indicates stall force of motors (5.7pN). The case with unsuccessful bundle formation (red) shows smaller $f_{\mathrm{M}}^{\max }$ and larger $f_{\mathrm{ACP}}^{\max }$ than the case with successful bundle formation (blue). (e) The maximum and (f) sustainability of tensile forces generated by bundles, depending on R_M and R_ACP. The sustainability ranges from 0 (not sustainable at all) to 1 (perfectly sustainable). Maximum force is positively correlated with both R_M and R_ACP. Sustainability is positively correlated with R_ACP but negatively correlated with R_M. (g) Compaction time as a measure of how rapidly networks transform into bundles. Networks compact faster with higher R_M and lower R_ACP. (h) Standard deviation of x positions of actins at compaction time (${\sigma }_x^{\text{c}}$) as a measure of how tightly the bundle is formed. Higher R_M and R_ACP leads to formation of tighter bundles.

Fig 3. Buckling of actin filaments plays a crucial role in bundle formation and tension generation.

(a) Number of actin filaments that experience buckling at least once during simulation depending on densities of motors (R_M) and ACPs (R_ACP), normalized by the largest number. Buckling takes place more frequently with higher R_M and lower R_ACP. (b-c) Snapshots showing actin density of networks where buckling is suppressed via a 100-fold increase in bending stiffness of actin filaments (κ_b,A). In both networks with (b) low (R_M = 0.08 and R_ACP = 0.01) and (c) high ACP density (R_M = 0.08 and R_ACP = 0.1), bundles were hardly formed. (d) Time evolution of generated tension (solid line) and the number of buckling events (dashed line) for cases with reference bending stiffness (blue triangle, κ_b,A = ${\kappa }_{\mathrm{b},\mathrm{A}}^{*}$) and 100-fold higher bending stiffness (red circle, κ_b,A = 100×${\kappa }_{\mathrm{b},\mathrm{A}}^{*}$) at R_M = 0.08 and R_ACP = 0.1. (e) Distribution of forces exerted on motors ($f_{\mathrm{M}}^{\max }$) and ACPs ($f_{\mathrm{ACP}}^{\max }$) measured at peak tension for cases shown in (d). The legend is shared with (d). (f) The maximum and (g) sustainability of tension measured from cases (κ_b,A = 100×${\kappa }_{\mathrm{b},\mathrm{A}}^{*}$) with various R_M and R_ACP. Compared to cases with reference bending stiffness (Fig 2E and 2F), the networks exhibit smaller maximum tension and higher sustainability, whereas proportionality to R_M and R_ACP is maintained. (h) Compaction time. (i) Standard deviation of x positions of actins at compaction time (${\sigma }_x^{\text{c}}$). Note that the lower limit of the color scaling is much larger than that in Fig 2H.

Fig 4. Initial orientation of actin filaments regulates bundle formation and tension generation.

Densities of motors (R_M) and ACPs (R_ACP) used in cases shown here are 0.08 and 0.01, respectively. (a-c) (1st column) Orientations where barbed ends of actin filaments in networks are initially directed. Red on the circles located at the bottom-right corner represents the range of the orientation. Arrows in the boxes represent examples of filaments with corresponding initial orientations. (2nd, 3rd, 4th columns) Snapshots showing actin density in the networks at t = 10, 30, and 60 s with initial orientation indicated in the 1st column. (5th column) Initial and final orientations of actin filaments. Final orientation indicates orientation of filaments measured at a time point when compaction time is defined. (d) Time evolution of tension for cases with biased initial orientations shown in (a-c) and isotropic initial orientation. (e) Number of buckling events occurring during simulations for cases shown in (d). (f) Time evolution of a fraction of antiparallel filament pairs for cases shown in (d).

Fig 5. In networks with biased filament orientation, parallel filament pairs can form bundles without buckling of filaments, whereas antiparallel pairs cannot.

Densities of motors (R_M) and ACPs (R_ACP) are 0.08 and 0.01, respectively as in Fig 4, but bending stiffness of actin filaments is increased 100-fold (κ_b,A = 100×${\kappa }_{\mathrm{b},\mathrm{A}}^{*}$). (a-c) (1st column) Initial orientations of actin filaments in networks. (2nd, 3rd, 4th columns) Snapshots showing actin density in the networks with initial filament orientation indicated in the 1st column. (5th column) Initial and final orientation of actin filaments. (d) Time evolution of tensile forces generated by bundles for cases with biased initial orientations shown in (a-c) and isotropic initial orientation. (e) Time evolution of a fraction of antiparallel filament pairs for cases shown in (d).

Fig 6. Actin turnover modulates bundle formation and tension generation.

Densities of motors (R_M) and ACPs (R_ACP) used in cases shown here are 0.08 and 0.01, respectively. (a-d) Snapshots showing actin density in networks (a) without actin turnover and (b-d) with actin turnover rate (k_t,A) of 60 s^-1. In networks with actin turnover, depolymerization of actin filaments was inhibited by bound ACPs or motors to an extent determined by inhibition factor (ξ_d,A). ξ_d,A ranges between 0 (no inhibition of depolymerization) and 1 (complete inhibition). In these examples, ξ_d,A is (b) 0, (c) 0.6, or (d) 1. (e) Time evolution of tensile forces generated by bundles for cases shown in (a-d). (f) The maximum and (g) sustainability of tension, depending on k_t,A and ξ_d,A. Maximum tension shows no correlation with k_t,A and ξ_d,A, whereas sustainability is higher at intermediate range of ξ_d,A. (h) Compaction time. (i) Standard deviation of x positions of actins at compaction time (${\sigma }_x^{\text{c}}$). With more turnover (i.e. high k_t,A and low ξ_d,A), bundles form faster, but the formed bundles are more loose.