Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Jan 27:7:41385.
doi: 10.1038/srep41385.

On the Fractality of Complex Networks: Covering Problem, Algorithms and Ahlfors Regularity

Lihong Wang  1   2 , Qin Wang  3 , Lifeng Xi  2 , Jin Chen  4 , Songjing Wang  2 , Liulu Bao  1 , Zhouyu Yu  5 , Luming Zhao  2
Affiliations

On the Fractality of Complex Networks: Covering Problem, Algorithms and Ahlfors Regularity

Lihong Wang et al. Sci Rep. .

Abstract

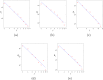
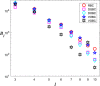
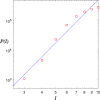
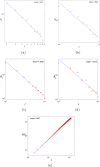
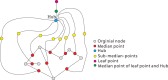
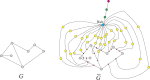
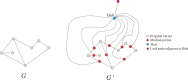
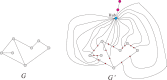
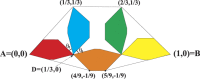
In this paper, we revisit the fractality of complex network by investigating three dimensions with respect to minimum box-covering, minimum ball-covering and average volume of balls. The first two dimensions are calculated through the minimum box-covering problem and minimum ball-covering problem. For minimum ball-covering problem, we prove its NP-completeness and propose several heuristic algorithms on its feasible solution, and we also compare the performance of these algorithms. For the third dimension, we introduce the random ball-volume algorithm. We introduce the notion of Ahlfors regularity of networks and prove that above three dimensions are the same if networks are Ahlfors regular. We also provide a class of networks satisfying Ahlfors regularity.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing financial interests.

Figures

Figure 1
Figure 1. Slopes exist w.r.t. 5 algorithms for the WWW network: (a) RBC, (b) DGBC, (c) DOBC, (d) VGBC, (e) VOBC.
Figure 2
Figure 2. Comparison of 5 algorithms for the WWW network.
Figure 3
Figure 3. RBV for the WWW network.
Figure 4
Figure 4. Rule 1.
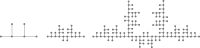
Figure 5
Figure 5. G1, G2, G3 of growing trees w.r.t. rule 1.
Figure 6
Figure 6. Fractal dimensions of G5: (a) CBB, (b) RBC, (c) DGBC, (d) DOBC, (e) RBV.
Figure 7
Figure 7. Rule 2.
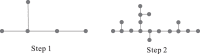
Figure 8
Figure 8. G1, G2 of growing trees w.r.t. rule 2.
Figure 9
Figure 9. The first three steps according to an infinite sequence .
Figure 10
Figure 10. The reduction process for l = 3.
Figure 11
Figure 11. The reduction process for l = 4.
Figure 12
Figure 12. The reduction process for l = 3.
Figure 13
Figure 13. The reduction process for l = 4.
Figure 14
Figure 14. The first two steps of self-similar fractal (model 1).
Figure 15
Figure 15. Step 4 of self-similar fractal (model 1).
Figure 16
Figure 16. OSC holds.
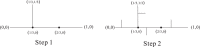
Figure 17
Figure 17. The first two steps of self-similar fractal of model 2.
Figure 18
Figure 18. Step 4 of self-similar fractal of model 2.
See this image and copyright information in PMC

References

    1. Watts D. J. & Strogatz S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998). - PubMed
    1. Barabási A. L. & Albert R. Emergence of scaling in random networks. Science 286, 509–512 (1999). - PubMed
    1. Newman M. E. J. The structure and function of complex networks. Siam Review 45, 167–256 (2003).
    1. Newman M. E. J. Networks: An Introduction. Oxford, Oxford University Press (2010).
    1. Song C., Havlin S. & Makse H. A. Self-similarity of complex networks. Nature 433, 392–395 (2005). - PubMed

Publication types

LinkOut - more resources