The dynamics of disease in a metapopulation: The role of dispersal range

Abstract

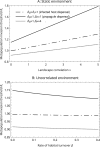
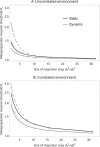
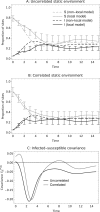
The establishment and spread of a disease within a metapopulation is influenced both by dynamics within each population and by the host and pathogen spatial processes through which they are connected. We develop a spatially explicit metapopulation model to investigate how the form of host and disease dispersal jointly influence the probability of disease establishment and invasion. We show that diseases are more likely to establish if both the host and the disease tend to disperse locally, since the former leads to the spatial aggregation of host populations in the environment while the latter facilitates the pathogen's exploitation of this spatial pattern. In contrast, local pathogen dispersal is likely to reduce the probability of subsequent disease spread because it increases the spatial segregation of infected and uninfected populations. The effects of local dispersal on disease dynamics are less pronounced when the pathogen spreads through the movement of infected hosts and more pronounced when pathogen dispersal is independent (for example through airborne viruses) though the details of host and pathogen biology can be important. These spatial effects tend to be more pronounced if the sites available for host occupation are themselves spatially aggregated.

Keywords: Correlated landscape; Disease; Dispersal kernel; Metapopulation; Spatial moments.

Fig. 1

The effect of host migration scale on the metapopulation invasion threshold $R_{*}$. If the disease spreads by dispersing pathogen propagules (dashed lines), low values of ${\delta }_P$ indicate the dispersal is local. For all the examples, the sites within the metapopulation have an uncorrelated and static distribution with average density 1, and the mean-field model (${\delta }_S={\delta }_I={\delta }_P=\infty$) predicts $R_{*}=1$. The parameters are $m_I=0.5,b=1.\dot{3},m_P=0$ for the infected host dispersal example, $m_I=0,m_P=1$ for the propagule dispersal cases and remaining parameters are $m_S=1,{\mu }_S=0.4,{\mu }_I=0.6$ for all cases. All examples use Gaussian dispersal kernels $D_X\left(\rho \right)=e^{-{\left(\frac{\rho }{{\delta }_X}\right)}^2}/\left(\pi {\delta }_X^2\right)\mathrm{for}X\in \left\{S,I,P\right\}$.

Fig. 2

Effects of underlying environmental structure on the metapopulation invasion threshold $R_{*}$. To approximate static environments (A) we set $\beta ={10}^{-8}$ and to approximate uncorrelated environments (B) we set $\nu ={10}^{-8}$. In each case $\alpha$ is varied along the x-axis so that the average density of sites, $\frac{\alpha \nu }{\beta }$, is always 1. The demographic parameters are the same as in Fig. 1 so that the non-local model predicts $R_{*}=1$, and the landscape kernel is Gaussian with length scale $\lambda =1$ ($K_{\lambda }\left(\rho \right)=e^{-{\rho }^2}/\pi$).

Fig. 3

The relative importance of infectiousness ($b$) and migration ($m_I$) for the spread of a disease that is transmitted by the movement of infected hosts. The non-local model predicts $R_{*}=1$ for each combination of $b$ and $m_I$ specified by the upper and lower scales on the x-axis. Other parameters are the same as in Fig. 1.

Fig. 4

Comparison of the first order approximations (lines) to finite-space simulations of a disease that spreads by the dispersal of pathogen propagules independent of the host. Parameters are the same as in Fig. 1, with equal host and disease length scales for each position on the x-axis (${\delta }_S={\delta }_P=\lambda$). The dispersal kernels $D_S\left(\rho \right)$ and $D_P\left(\rho \right)$ are 'top-hat' ($D_X\left(\rho \right)=\frac{1}{\pi {\delta }_X^2}$ if ${\rho <\delta }_X$ or 0 otherwise) and the landscape kernel is Gaussian. The error bars show $\pm 1$ standard error either side of the simulation means.

Fig. 5

The dynamics of an invasion in an uncorrelated static environment (A; $\nu \approx 0$) and a correlated static environment (B; $\nu =4,\lambda =0.5$). We assume the disease spreads by the dispersal of pathogen propagules, with parameters so that invasion is likely ($m_S=2,m_I=0,m_P=2,{\mu }_S=0.3,{\mu }_I=0.6$ giving $R_{*}^{\left(0\right)}=2.753$). In the upper plots, the solid lines plot the dynamics derived from the first order perturbation approximation, the dashed lines plot the dynamics from the equivalent non-local model and the bars plot the mean and standard errors of simulation results. The lower plot shows the covariance between susceptible and infected populations (${{\Gamma }_{\mathit{SI}}^P}^{\left(1\right)}$) for the two invasion scenarios. The dispersal kernels are top-hat and the landscape kernel is Gaussian.

Fig. 6

The effect of environmental correlation on the equilibrium densities of infected and susceptible populations. Parameters are A: $m_S=1,m_I=0.75,b=1,{\mu }_S=0.4,{\mu }_I=0.6,\lambda =0.5$; B: $m_S=2,m_I=0,m_P=2,{\mu }_S=0.3,{\mu }_I=0.6,\lambda =0.5$. The dispersal and landscape kernels are all Gaussian.