A radiobiological model of radiotherapy response and its correlation with prognostic imaging variables
- PMID: 28140359
- PMCID: PMC5512557
- DOI: 10.1088/1361-6560/aa5d42
A radiobiological model of radiotherapy response and its correlation with prognostic imaging variables
Abstract
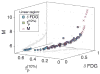
Radiobiological models of tumour control probability (TCP) can be personalized using imaging data. We propose an extension to a voxel-level radiobiological TCP model in order to describe patient-specific differences and intra-tumour heterogeneity. In the proposed model, tumour shrinkage is described by means of a novel kinetic Monte Carlo method for inter-voxel cell migration and tumour deformation. The model captures the spatiotemporal evolution of the tumour at the voxel level, and is designed to take imaging data as input. To test the performance of the model, three image-derived variables found to be predictive of outcome in the literature have been identified and calculated using the model's own parameters. Simulating multiple tumours with different initial conditions makes it possible to perform an in silico study of the correlation of these variables with the dose for 50% tumour control ([Formula: see text]) calculated by the model. We find that the three simulated variables correlate with the calculated [Formula: see text]. In addition, we find that different variables have different levels of sensitivity to the spatial distribution of hypoxia within the tumour, as well as to the dynamics of the migration mechanism. Finally, based on our results, we observe that an adequate combination of the variables may potentially result in higher predictive power.
Figures





Similar articles
-
Coupling I-125 permanent implant prostate brachytherapy Monte Carlo dose calculations with radiobiological models.Med Phys. 2017 Aug;44(8):4329-4340. doi: 10.1002/mp.12306. Epub 2017 Jul 12. Med Phys. 2017. PMID: 28455849
-
A voxel-based multiscale model to simulate the radiation response of hypoxic tumors.Med Phys. 2015 Jan;42(1):90-102. doi: 10.1118/1.4903298. Med Phys. 2015. PMID: 25563250
-
A TCP-NTCP estimation module using DVHs and known radiobiological models and parameter sets.J Appl Clin Med Phys. 2004 Winter;5(1):50-63. doi: 10.1120/jacmp.v5i1.1970. Epub 2004 Jan 1. J Appl Clin Med Phys. 2004. PMID: 15753933 Free PMC article.
-
Monte Carlo role in radiobiological modelling of radiotherapy outcomes.Phys Med Biol. 2012 Jun 7;57(11):R75-97. doi: 10.1088/0031-9155/57/11/R75. Epub 2012 May 9. Phys Med Biol. 2012. PMID: 22571871 Review.
-
Linear quadratic and tumour control probability modelling in external beam radiotherapy.J Math Biol. 2009 Apr;58(4-5):799-817. doi: 10.1007/s00285-008-0222-y. Epub 2008 Sep 30. J Math Biol. 2009. PMID: 18825382 Review.
Cited by
-
Stochastic multicellular modeling of x-ray irradiation, DNA damage induction, DNA free-end misrejoining and cell death.Sci Rep. 2019 Dec 11;9(1):18888. doi: 10.1038/s41598-019-54941-1. Sci Rep. 2019. PMID: 31827107 Free PMC article.
-
The relative biological effectiveness of carbon ion radiation therapy for early stage lung cancer.Radiother Oncol. 2020 Dec;153:265-271. doi: 10.1016/j.radonc.2020.09.027. Epub 2020 Sep 23. Radiother Oncol. 2020. PMID: 32976878 Free PMC article.
-
Radiotherapy Side Effects: Comprehensive Proteomic Study Unraveled Neural Stem Cell Degenerative Differentiation upon Ionizing Radiation.Biomolecules. 2022 Nov 26;12(12):1759. doi: 10.3390/biom12121759. Biomolecules. 2022. PMID: 36551187 Free PMC article.
-
Predicting and monitoring response to head and neck cancer radiotherapy using multimodality imaging and radiobiological digital twin simulations.Phys Med Biol. 2025 May 27;70(11):10.1088/1361-6560/add9de. doi: 10.1088/1361-6560/add9de. Phys Med Biol. 2025. PMID: 40378867
-
Data Science Opportunities To Improve Radiotherapy Planning and Clinical Decision Making.Semin Radiat Oncol. 2024 Oct;34(4):379-394. doi: 10.1016/j.semradonc.2024.07.012. Semin Radiat Oncol. 2024. PMID: 39271273 Free PMC article. Review.
References
-
- Antipas VP, Stamatakos GS, Uzunoglu NK, Dionysiou DD, Dale RG. A spatio-temporal simulation model of the response of solid tumours to radiotherapy in vivo: parametric validation concerning oxygen enhancement ratio and cell cycle duration. Physics in medicine and biology. 2004;49(8):1485–504. - PubMed
-
- van Baardwijk A, et al. Time trends in the maximal uptake of FDG on PET scan during thoracic radiotherapy. A prospective study in locally advanced non-small cell lung cancer (NSCLC) patients. Radiotherapy and Oncology. 2007;82(2):145–152. - PubMed
-
- Baert AL, Hermans R. Head and neck cancer imaging. Springer Science & Business Media; 2006.
-
- Bortz A, Kalos M, Lebowitz J. A new algorithm for Monte Carlo simulation of Ising spin systems. Journal of Computational Physics. 1975;17(1):10–18.
-
- Brenner DJ, Hlatky LR, Hahnfeldt PJ, Huang Y, Sachs RK. The linear-quadratic model and most other common radiobiological models result in similar predictions of time-dose relationships. Radiation research. 1998;150(1):83–91. arXiv: NIHMS150003. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
