Coevolutionary dynamics of phenotypic diversity and contingent cooperation

Abstract

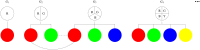
Phenotypic diversity is considered beneficial to the evolution of contingent cooperation, in which cooperators channel their help preferentially towards others of similar phenotypes. However, it remains largely unclear how phenotypic variation arises in the first place and thus leads to the construction of phenotypic complexity. Here we propose a mathematical model to study the coevolutionary dynamics of phenotypic diversity and contingent cooperation. Unlike previous models, our model does not assume any prescribed level of phenotypic diversity, but rather lets it be an evolvable trait. Each individual expresses one phenotype at a time and only the phenotypes expressed are visible to others. Moreover, individuals can differ in their potential of phenotypic variation, which is characterized by the number of distinct phenotypes they can randomly switch to. Each individual incurs a cost proportional to the number of potentially expressible phenotypes so as to retain phenotypic variation and expression. Our results show that phenotypic diversity coevolves with contingent cooperation under a wide range of conditions and that there exists an optimal level of phenotypic diversity best promoting contingent cooperation. It pays for contingent cooperators to elevate their potential of phenotypic variation, thereby increasing their opportunities of establishing cooperation via novel phenotypes, as these new phenotypes serve as secret tags that are difficult for defector to discover and chase after. We also find that evolved high levels of phenotypic diversity can occasionally collapse due to the invasion of defector mutants, suggesting that cooperation and phenotypic diversity can mutually reinforce each other. Thus, our results provide new insights into better understanding the coevolution of cooperation and phenotypic diversity.

Fig 1. Phenotypic diversity and contingent cooperation.

We consider variation in the capacity of expressing different phenotypes. G₁ possesses only one expressible phenotype, say Red. G₄ possesses four expressible phenotypes, say Red, Green, Blue and Yellow. Each individual just expresses one phenotype. G₂ can express either Red or Blue, while G₃ can express Red, Blue or Green. When G₂ and G₃ express the same phenotype, there will be an interaction (solid line) between them. When they express different phenotypes, there will be no interaction between them. The interaction outcome is dependent on their strategic behaviors. When both are cooperators, they each get the benefit b − c. When both are defectors, they get zero payoff each. When a cooperator meets a defector, the former gets the payoff −c, while the later reaps the payoff b.

Fig 2. Pairwise invasion plots.

Transition rate means the probability that the population moves from an invaded state to an invading state. The capital letter, C or D, along the Y-axis, denotes the mutant’s behavioral strategy, while the one along the X-axis denotes the residents’ behavioral strategy. The coordinate value denotes the number of potentially expressible phenotypes that individuals are endowed with. Parameters: N = 20, b = 1, c = 0.3, β = 0.1, θ = 0.1.

Fig 3. Stationary distribution for 2M competing strains.

Fraction of these 2M strains in the long run. The bars are obtained by solving the eigenvector of the 2M by 2M transition matrix. Empty circles and empty triangles are obtained by simulations. Blue denotes cooperator, and red defector. The abscissa value represents how many potentially expressible phenotypes individuals can switch to. The evolutionary process is fully characterized in the main text. Parameters: N = 20, b = 1, c = 0.3, β = 0.1, μ = 0.002. From A to F, θ is 0, 0.05, 0.1, 0.3, 0.5, 1, correspondingly, and the overall cooperation level is 0.91, 0.88, 0.84, 0.63, 0.49, and 0.29, respectively.

Fig 4. Time evolution of the competition between cooperative strains and defective strains.

When the population is occupied by defective strain, it is most likely that the defective strain possesses a very small number of potentially expressible phenotypes. It is either followed by the invasion of defective strain with similar numbers of phenotypes, or by cooperative strain with a moderate number of phenotypes. In the former case, the evolutionary process advances just as it starts. In the later case, it gets very hard for the cooperative strain to be invaded, since it possesses the strongest resistance power against invasion of other strains. In the average sense, cooperative strain endowed with a moderate number of phenotypes prevails most of the time. Parameters: N = 20, b = 1, c = 0.3, β = 0.1, μ = 0.002, and θ = 0.1.

Fig 5. Cooperation level, the optimal phenotypic diversity of cooperative strain as a function of θ and β, respectively.

The overall cooperation level decreases with θ. So does the optimal diversity. Even when cooperation is disfavored, the optimal diversity of all cooperative strains still exists. Quite differently, there exists an optimal selection intensity at which the overall cooperation level arrives at the highest and, correspondingly the optimum of diversity level is maximized. Parameters: N = 20, b = 1, c = 0.3. In panels A and B β = 0.1. In panels C and D θ = 0.1.