Analysis of a mechanistic Markov model for gene duplicates evolving under subfunctionalization
- PMID: 28143390
- PMCID: PMC5282866
- DOI: 10.1186/s12862-016-0848-0
Analysis of a mechanistic Markov model for gene duplicates evolving under subfunctionalization
Abstract
Background: Gene duplication has been identified as a key process driving functional change in many genomes. Several biological models exist for the evolution of a pair of duplicates after a duplication event, and it is believed that gene duplicates can evolve in different ways, according to one process, or a mix of processes. Subfunctionalization is one such process, under which the two duplicates can be preserved by dividing up the function of the original gene between them. Analysis of genomic data using subfunctionalization and related processes has thus far been relatively coarse-grained, with mathematical treatments usually focusing on the phenomenological features of gene duplicate evolution.
Results: Here, we develop and analyze a mathematical model using the mechanics of subfunctionalization and the assumption of Poisson rates of mutation. By making use of the results from the literature on the Phase-Type distribution, we are able to derive exact analytical results for the model. The main advantage of the mechanistic model is that it leads to testable predictions of the phenomenological behavior (instead of building this behavior into the model a priori), and allows for the estimation of biologically meaningful parameters. We fit the survival function implied by this model to real genome data (Homo sapiens, Mus musculus, Rattus norvegicus and Canis familiaris), and compare the fit against commonly used phenomenological survival functions. We estimate the number of regulatory regions, and rates of mutation (relative to silent site mutation) in the coding and regulatory regions. We find that for the four genomes tested the subfunctionalization model predicts that duplicates most-likely have just a few regulatory regions, and the rate of mutation in the coding region is around 5-10 times greater than the rate in the regulatory regions. This is the first model-based estimate of the number of regulatory regions in duplicates.
Conclusions: Strong agreement between empirical results and the predictions of our model suggest that subfunctionalization provides a consistent explanation for the evolution of many gene duplicates.
Keywords: Continuous-time Markov chain (CTMC); Gene duplication; Neofunctionalization; Nonfunctionalization; Phase-type distribution; Pseudogenization; Subfunctionalization.
Figures
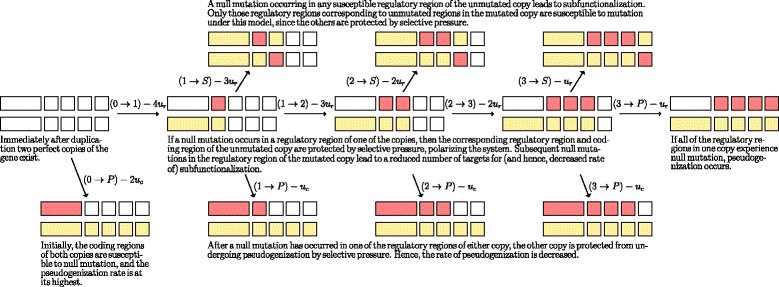
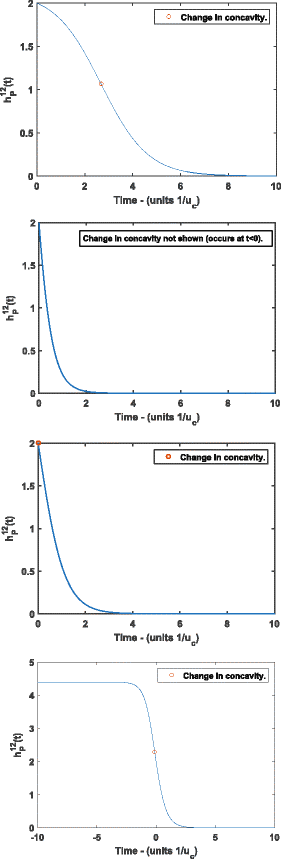
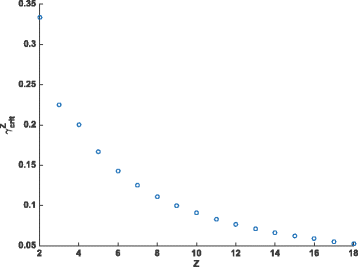


References
-
- Innan H, Kondrashov F. The evolution of gene duplications: classifying and distinguishing between models. Nat Rev Genet. 2010;11(2):97–108. - PubMed
-
- Liberles DA, Kolesov G, Dittmar K. Evolution after Gene Duplication. In: Dittmar K, Liberles D, editors. Hoboken: Wiley : 2010. doi:10.1002/9780470619902.ch1. - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

