A predictive assessment of genetic correlations between traits in chickens using markers

Abstract

Background: Genomic selection has been successfully implemented in plant and animal breeding programs to shorten generation intervals and accelerate genetic progress per unit of time. In practice, genomic selection can be used to improve several correlated traits simultaneously via multiple-trait prediction, which exploits correlations between traits. However, few studies have explored multiple-trait genomic selection. Our aim was to infer genetic correlations between three traits measured in broiler chickens by exploring kinship matrices based on a linear combination of measures of pedigree and marker-based relatedness. A predictive assessment was used to gauge genetic correlations.

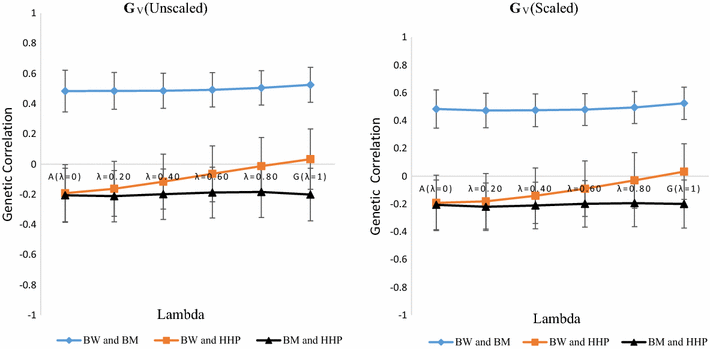
Methods: A multivariate genomic best linear unbiased prediction model was designed to combine information from pedigree and genome-wide markers in order to assess genetic correlations between three complex traits in chickens, i.e. body weight at 35 days of age (BW), ultrasound area of breast meat (BM) and hen-house egg production (HHP). A dataset with 1351 birds that were genotyped with the 600 K Affymetrix platform was used. A kinship kernel (K) was constructed as K = λ G + (1 - λ)A, where A is the numerator relationship matrix, measuring pedigree-based relatedness, and G is a genomic relationship matrix. The weight (λ) assigned to each source of information varied over the grid λ = (0, 0.2, 0.4, 0.6, 0.8, 1). Maximum likelihood estimates of heritability and genetic correlations were obtained at each λ, and the "optimum" λ was determined using cross-validation.

Results: Estimates of genetic correlations were affected by the weight placed on the source of information used to build K. For example, the genetic correlation between BW-HHP and BM-HHP changed markedly when λ varied from 0 (only A used for measuring relatedness) to 1 (only genomic information used). As λ increased, predictive correlations (correlation between observed phenotypes and predicted breeding values) increased and mean-squared predictive error decreased. However, the improvement in predictive ability was not monotonic, with an optimum found at some 0 < λ < 1, i.e., when both sources of information were used together.

Conclusions: Our findings indicate that multiple-trait prediction may benefit from combining pedigree and marker information. Also, it appeared that expected correlated responses to selection computed from standard theory may differ from realized responses. The predictive assessment provided a metric for performance evaluation as well as a means for expressing uncertainty of outcomes of multiple-trait selection.

Fig. 1

Scatter plots of phenotypes pre-corrected for non-genetic sources of variation for body weight (BW), breast muscle area (BM) and hen-house production (HHP)

Fig. 2

Average and standard errors estimates of genetic and genomic correlations across 20 replicates between body weight (BW), breast meat (BM) and hen-house production (HHP) as a function of the weight placed on Forni’s genomic relationship matrix G _F (λ)

Fig. 3

Average and standard errors estimates of genetic and genomic correlations across 20 replicates between body weight (BW), breast meat (BM) and hen-house production (HHP) as a function of the weight placed on VanRaden’s genomic relationship matrix G _V (λ)

Fig. 4

Boxplot of predictive correlations across 20 replicates between phenotypes and predicted breeding values (upper two rows), and of mean squared errors (MSE) (bottom two rows) in testing sets. Red and light blue colors denote values for unscaled and scaled relationship matrices of Forni or VanRaden, respectively. Outliers are denoted as black dots, and the x-axis label denotes λ = 0, 0.2, 0.4, 0.6, 0.8, 1

Fig. 5

Scatter plots of the regression coefficient of observed phenotype for BW on DGV of BM; $b_{y\left(BW\right),DGV\left(BM\right)}$ (first row), and the regression of observed phenotype for BM on DGV of BW; $b_{y\left(BM\right),DGV\left(BW\right)}$ (second row) in the testing set for 20 cross-validated (CV) regression coefficients. The red dots are expected genetic regressions from REML analyses conducted at each λ. The x-axis label denotes λ = 0, 0.2, 0.4, 0.6, 0.8, 1. DGV: direct genomic values; GFU: unscaled Forni’s G; GFS: scaled Forni’s G; GVU: unscaled VanRaden’s G; GVS: scaled VanRaden’s G. Dark blue points show the median of regressions for 20 random samples

Fig. 6

Scatter plot of the regression coefficient of observed phenotype for BW on DGV of HHP; $b_{y\left(BW\right),DGV\left(HHP\right)}$ (first row) and the regression of observed phenotype for HHP on DGV of BW; $b_{y\left(HHP\right),DGV\left(BW\right)}$ (second row) in testing set for 20 cross-validated (CV) regression coefficients. The red dots are expected genetic regressions from REML analyses conducted at each λ = (0, 0.2, 0.4, 0.6, 0.8, 1). The x-axis label denotes λ = 0, 0.2, 0.4, 0.6, 0.8, 1. GFU: unscaled Forni’s G; GFS: scaled Forni’s G; GVU: unscaled VanRaden’s G; GVS: scaled VanRaden’s G. Dark blue points show the median of regression coefficients for 20 random samples

Fig. 7

Scatter plots of the regression of observed phenotype for BM on DGV of HHP; $b_{y\left(BM\right),DGV\left(HHP\right)}$, (first row) and the regression of observed phenotype for HHP on DGV of BW $b_{y\left(HHP\right),DGV\left(BM\right)}$, (second row) in testing set for 20 cross-validated (CV) regression coefficients. Red dots are expected genetic regressions from REML analyses conducted at each λ. The x-axis label denotes λ = 0, 0.2, 0.4, 0.6, 0.8, 1. GFU: unscaled Forni’s G; GFS: scaled Forni’s G; GVU: unscaled VanRaden’s G; GVS: scaled VanRaden’s G. Dark blue points show the median of regressions for 20 random samples