Robust network topologies for generating oscillations with temperature-independent periods

Abstract

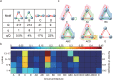
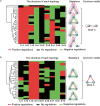
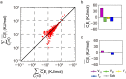
Nearly all living systems feature a temperature-independent oscillation period in circadian clocks. This ubiquitous property occurs at the system level and is rooted in the network architecture of the clock machinery. To investigate the mechanism of this prominent property of the circadian clock and provide general guidance for generating robust genetic oscillators with temperature-compensated oscillations, we theoretically explored the design principle and core network topologies preferred by oscillations with a temperature-independent period. By enumerating all topologies of genetic regulatory circuits with three genes, we obtained four network motifs, namely, a delayed negative feedback oscillator, repressilator, activator-inhibitor oscillator and substrate-depletion oscillator; hybrids of these motifs constitute the vast majority of target network topologies. These motifs are biased in their capacities for achieving oscillations and the temperature sensitivity of the period. The delayed negative feedback oscillator and repressilator are more robust for oscillations, whereas the activator-inhibitor and substrate-depletion oscillators are superior for maintaining a temperature-independent oscillation period. These results suggest that thermally robust oscillation can be more plausibly achieved by hybridizing these two categories of network motifs. Antagonistic balance and temperature insulation mechanisms for achieving temperature compensation are typically found in these topologies with temperature robustness. In the temperature insulation approach, the oscillation period relies on very few parameters, and these parameters are influenced only slightly by temperature. This approach prevents the temperature from affecting the oscillation period and generates circadian rhythms that are robust against environmental perturbations.

Fig 1. The overall performance of TCO networks.

(a) Distribution of oscillatory topologies in Q-q-value space. Red triangles represent networks with at least one circuit with TCO, i.e., q-value > 0; blue circles are for oscillatory networks that do not have TCO parameters, i.e., q-value = 0. Robust topologies with top q-values (q-value > 8) are highlighted in the upper frame, which surrounds 35 networks that are best for TCO. There are another 35 “worst” topologies that are not thermally robust (q-value = 0) but have high Q-values (Q-value > 40), as marked by the lower frame. (b) The TCO topologies in (a) are re-plotted in the space of q-value and number of links (k). The circle size is proportional to the number of topologies with a specific (q, k) combination. The best TCO topologies are highlighted again in the upper frame. Topologies with the least number of links (k = 3) are emphasized in the low square.

Fig 2. Structure decomposition of TCO networks.

(a) The simplest network motifs with TCO, namely, delayed negative feedback oscillator (motif A), repressilator (motif B), activator-inhibitor (motif C) and substrate-depletion (motif D). Motifs A and B have relatively larger Q but smaller q/Q ratio compared with motifs C and D. (b) The distribution of TCO topologies in the q-value-and-motif-combination space coded by color. TCO topologies that do not contain any of motifs A, B, C, or D are classified as E-class (shown at the right end of the horizontal axis). The sum of topologies in each q-value range is shown on the right. The percentage of each type of circuit architecture in the corresponding q-value range is coded in color. Due to structural conflict in regulations, motif B and motif D cannot coexist in a three-node network so that combinations BD, ABD, BCD, ABCD (and similarly motif A and motif B combinations) are not permitted. (c) Several examples of TCO topologies composed of simple motifs or their combinations: C, BC, AC, ABC, ACD, together with one that falls in the E-class. The green, blue, pink and yellow areas denote motifs A, B, C and D, respectively.

Fig 3. Clustering of best and worst oscillatory networks for temperature compensation.

(a) Clustering of 35 TCO networks with top q-values. (b) Clustering of 35 worst TCO networks with top Q-values but a zero q-value. Positive, negative and null regulations between the nodes are denoted by red, green and black, respectively. Each row demonstrates the interaction combination between Nodes 1, 2, 3 in a network. The skeletons depict typical network topologies and motif constituents as revealed in the clustering of both the best and worst TCO topologies, respectively. The right motifs C and A show individually the most common core structures in the two categories of networks.

Fig 4. Control coefficients for simple TCO motifs.

The temperature dependence of the control coefficient C_i (defined as ∂lnP/∂lnk_i), which measures the parameter sensitivity of the oscillation period, is depicted for motifs A (a₁, a₂), B (b₁, b₂), C (c₁, c₂) and D (d₁, d₂), respectively, with each topology having two sets of parameters for TCOs. The parameter values used in our calculation of these TCOs are provided in the S1 Text.

Fig 5. Achieving TCOs in motif C.

(a) Averaged control coefficient ${\overline{C}}_i$ over the examined temperature range for different parameter combinations. The error bar is the standard deviation. The horizontal axis is the index for circuits with different TCO parameters for motif C. The decay rate constant r₂ has the largest amplitude and dominates the oscillation period. The data were obtained by computations of 100,000 parameter samplings. (b) The activation energies for the rate constants corresponding to the control coefficients in (a). The activation energies for r₂ fall primarily on the bottom. (c) is the product $\overline{C_i}{E}_i$ of the data in (a) and (b).

Fig 6. Mechanism of temperature compensation.

(a) Accumulation of C_iE_i with C_i > 0 plotted against that with C_i < 0 for 398 different TCO realizations in the 35 best TCO topologies. The sums ${\displaystyle {\sum }_{C_i>0}{C}_i{E}_i}$ and ${\displaystyle {\sum }_{C_i<0}{C}_i{E}_i}$ are averaged over the examined temperature range and plotted in logarithmic scale with an inverted horizontal axis. (b) The mean C_iE_is corresponding to the C_i~T dependencies in Fig 4c₁. (c) The mean C_iE_is corresponding to the C_i~T dependencies in Fig 4c₂. The averages were calculated over the temperature range [283K, 303K].