On the dynamical structure of calcium oscillations

Abstract

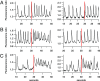
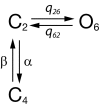
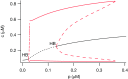
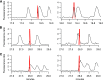
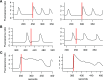
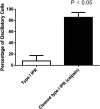
Oscillations in the concentration of free cytosolic Ca²⁺ are an important and ubiquitous control mechanism in many cell types. It is thus correspondingly important to understand the mechanisms that underlie the control of these oscillations and how their period is determined. We show that Class I Ca²⁺ oscillations (i.e., oscillations that can occur at a constant concentration of inositol trisphosphate) have a common dynamical structure, irrespective of the oscillation period. This commonality allows the construction of a simple canonical model that incorporates this underlying dynamical behavior. Predictions from the model are tested, and confirmed, in three different cell types, with oscillation periods ranging over an order of magnitude. The model also predicts that Ca²⁺ oscillation period can be controlled by modulation of the rate of activation by Ca²⁺ of the inositol trisphosphate receptor. Preliminary experimental evidence consistent with this hypothesis is presented. Our canonical model has a structure similar to, but not identical to, the classic FitzHugh-Nagumo model. The characterization of variables by speed of evolution, as either fast or slow variables, changes over the course of a typical oscillation, leading to a model without globally defined fast and slow variables.

Keywords: cytosolic calcium concentration modeling, multiple time scales; inositol trisphosphate receptor; mathematical modeling.

Fig. 1.

Pulse responses of the model with $p_s=\mathrm{\hspace{0.17em}0.12}$. (A, C, and E) Time courses of the response. The pulse occurs at the blue line. (B, D, and F) Solutions in the phase space. The blue and green surfaces represent, respectively, unstable and stable limit cycles of the model for constant $p$. The red curve shows steady states of the model for constant $p$ (solid for stable, dashed for unstable), and HB denotes a Hopf bifurcation of these steady states. The solid black line indicates the section of the model solution that occurs during the ${\text{IP}}_3$ pulse. (A and B) The ${\text{IP}}_3$ pulse pushes the solution to a point from where it is attracted to the green surface of stable periodic solutions, whereupon oscillations occur immediately, with a higher frequency. (C and D) When the pulse occurs on the lower portions of the downstroke of the ${\text{Ca}}^{2+}$ spike, the trajectory is pushed to a position where it is attracted to the lower part of the green surface, whereupon it must traverse this lower surface before the next spike can occur. (E and F) When the pulse occurs slightly higher on the downstroke, the trajectory is pushed toward the branch of stable steady states, resulting in small oscillations on a plateau, which change back to larger oscillations once the trajectory passes through the Hopf bifurcation point at the end of the Hopf trumpet.

Fig. 2.

Responses of HSY cells. ${\text{Ca}}^{2+}$ oscillations were initiated by ATP, and a pulse of exogenous ${\text{IP}}_3$ was applied at the vertical red line. For A–C, the left and right graphs are two examples of the same type of response. (A) When the pulse occurs between ${\text{Ca}}^{2+}$ spikes, it causes an immediate spike and an increase in oscillation frequency. (B) When the pulse occurs soon after a ${\text{Ca}}^{2+}$ spike, there is no immediate response, but, after a delay, the oscillations resume with a higher frequency. (C) When the pulse occurs close to the peak of the ${\text{Ca}}^{2+}$ spike, it causes smaller amplitude oscillations on a raised but decreasing baseline. For more details of the experimental results, see Supporting Information.

Fig. 3.

Responses of ASMCs. Ca²⁺ oscillations were initiated by methacholine, and a pulse of exogenous IP₃ was applied at the vertical red line. For A–C, the left and right graphs are two examples of the same type of response. The three different types of responses in A–C are as described in the legend of Fig. 2. For more details of the experimental results, see Supporting Information.

Fig. 4.

Responses of DT40-3KO cells, with transfected type II IPRs. Ca²⁺ oscillations were initiated by 50 nM trypsin, and a pulse of exogenous IP₃ was applied at the vertical red line. For A–C, the left and right graphs are two examples of the same type of response. The three different types of responses in A–C are as described in the legend of Fig. 2. For more details of the experimental results, see Supporting Information.

Fig. 5.

(A) Responses to anti-IgM of DT40-3KO cells, transfected with type I IPRs. Anti-IgM was added at 100 s in the experimental traces [cleaved IPRs (calpain) (Left) and wild type (Right)]. (B) Model responses. Here, $p$ was increased from 0 to $0.1\mu \text{M}$ at 0 s [${\tau }_{\text{max}}=1\text{,}000$ (Left) and ${\tau }_{\text{max}}=100\text{,}000$ (Right)]. These experiments were done before the model construction and therefore are not tests of model predictions.

Fig. S3.

Oscillation period as a function of ${\tau }_{\text{max}}$, plotted at a constant $p=\mathrm{\hspace{0.17em}0.1}$. As ${\tau }_{\text{max}}$ is increased from 1, oscillations appear in a Hopf bifurcation at ${\tau }_{\text{max}}=30.2$.

Fig. S1.

Schematic diagram of the IPR model of ref. , which is based on a simplification of the model of ref. . Here, $\beta$ and $\alpha$ are functions of $c$ and $p$, determined by fitting to single-channel data. $\beta$ is also a function of time, via the variable $h$, but the parameters governing $h$ were not determined by fitting to single-channel data. Instead, they were estimated from ref. .

Fig. S2.

Bifurcation diagram of the model. HB denotes a Hopf bifurcation; black curves are steady states (solid for stable, dashed for unstable); and red curves show the maximum and minimum values of $c$ on limit cycles (solid for stable, dashed for unstable).

Fig. S4.

(A) Plots of $(t_a-t_f)/T_b$ against $(t_f-t_b)/T_b$, as defined in the text, for three different cell types, compared with the model prediction. Both the data and the model show a clear decreasing trend, with hyperbolic shape. (B) Plot of $T=T_a/T_b$, the postflash oscillation period divided by the preflash oscillation period, determined from those cells where it was possible to determine the pre and postflash periods.

Fig. S5.

(A–C) Plots of experimental time traces from HSY cells (Fig. 2) redrawn on an expanded time scale, so the positioning of the flash is clearer. The red curve shows the timing of the flash that releases ${\text{IP}}_3$, and the black curve shows the fluorescence ratio. In A and B, the sharp spike in the black curve, which occurs at exactly the same time as the pulse, is not $[{\text{Ca}}^{2+}]$ but is an artifact of the flash.

Fig. S6.

A–C) Plots of experimental time traces from ASMCs (Fig. 3) redrawn on an expanded time scale, so the positioning of the flash is clearer.

Fig. S7.

(A–C) Plots of experimental time traces from DT40-3KO cells (Fig. 4) redrawn on an expanded time scale, so the positioning of the flash is clearer.

Fig. S8.

Percentage of oscillatory DT40-3KO cells with cleaved type I IPRs compared with normal type I IPRs.