Coalescence of Black Hole-Neutron Star Binaries
- PMID: 28163619
- PMCID: PMC5255529
- DOI: 10.12942/lrr-2011-6
Coalescence of Black Hole-Neutron Star Binaries
Abstract
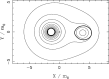
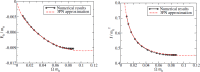
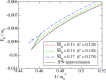
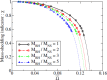
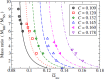
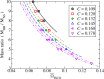
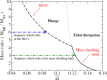
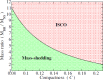
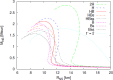
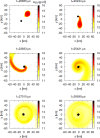
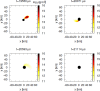
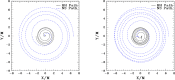
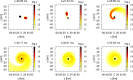
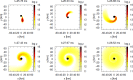
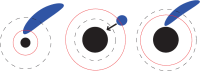
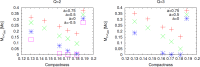
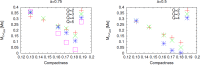
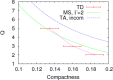
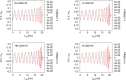
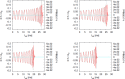
We review the current status of general relativistic studies for the coalescence of black hole-neutron star (BH-NS) binaries. First, procedures for a solution of BH-NS binaries in quasi-equilibrium circular orbits and the numerical results, such as quasi-equilibrium sequence and mass-shedding limit, of the high-precision computation, are summarized. Then, the current status of numerical-relativity simulations for the merger of BH-NS binaries is described. We summarize our understanding for the merger and/or tidal disruption processes, the criterion for tidal disruption, the properties of the remnant formed after the tidal disruption, gravitational waveform, and gravitational-wave spectrum.
Figures




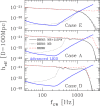


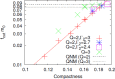


References
-
- Abadie J, LIGO Scientific Collaboration et al. Calibration of the LIGO Gravitational Wave Detectors in the Fifth Science Run. Nucl. Instrum. Methods A. 2010;624:223–240. doi: 10.1016/j.nima.2010.07.089. - DOI
-
- Abbott BP, LIGO Scientific Collaboration et al. LIGO: the Laser Interferometer Gravitational-Wave Observatory. Rep. Prog. Phys. 2009;72:076901. doi: 10.1088/0034-4885/72/7/076901. - DOI
-
- Accadia T, Virgo Collaboration et al. Calibration and sensitivity of the Virgo dector during its second science run. Class. Quantum Grav. 2011;28:025005. doi: 10.1088/0264-9381/28/2/025005. - DOI
-
- Acernese F, Virgo Collaboration et al. Status of VIRGO. Class. Quantum Grav. 2008;25:114045. doi: 10.1088/0264-9381/25/11/114045. - DOI
-
- Ajith P, et al. Template bank for gravitational waveforms from coalescing binary black holes: Nonspinning binaries. Phys. Rev. D. 2008;77:104017. doi: 10.1103/PhysRevD.77.104017. - DOI
Publication types
LinkOut - more resources
Full Text Sources
Miscellaneous
