Dynamical Boson Stars
- PMID: 28163621
- PMCID: PMC5254209
- DOI: 10.12942/lrr-2012-6
Dynamical Boson Stars
Abstract
The idea of stable, localized bundles of energy has strong appeal as a model for particles. In the 1950s, John Wheeler envisioned such bundles as smooth configurations of electromagnetic energy that he called geons, but none were found. Instead, particle-like solutions were found in the late 1960s with the addition of a scalar field, and these were given the name boson stars. Since then, boson stars find use in a wide variety of models as sources of dark matter, as black hole mimickers, in simple models of binary systems, and as a tool in finding black holes in higher dimensions with only a single Killing vector. We discuss important varieties of boson stars, their dynamic properties, and some of their uses, concentrating on recent efforts.
Figures




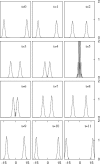
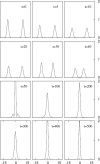
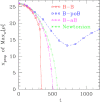

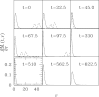
Similar articles
-
Dynamical boson stars.Living Rev Relativ. 2017;20(1):5. doi: 10.1007/s41114-017-0007-y. Epub 2017 Nov 13. Living Rev Relativ. 2017. PMID: 29200936 Free PMC article. Review.
-
GW190521 as a Merger of Proca Stars: A Potential New Vector Boson of 8.7×10^{-13} eV.Phys Rev Lett. 2021 Feb 26;126(8):081101. doi: 10.1103/PhysRevLett.126.081101. Phys Rev Lett. 2021. PMID: 33709746
-
Kerr black holes with scalar hair.Phys Rev Lett. 2014 Jun 6;112(22):221101. doi: 10.1103/PhysRevLett.112.221101. Epub 2014 Jun 2. Phys Rev Lett. 2014. PMID: 24949750
-
Great Impostors: Extremely Compact, Merging Binary Neutron Stars in the Mass Gap Posing as Binary Black Holes.Phys Rev Lett. 2020 Feb 21;124(7):071101. doi: 10.1103/PhysRevLett.124.071101. Phys Rev Lett. 2020. PMID: 32142310
-
Relativistic Binaries in Globular Clusters.Living Rev Relativ. 2013;16(1):4. doi: 10.12942/lrr-2013-4. Epub 2013 Mar 4. Living Rev Relativ. 2013. PMID: 28179843 Free PMC article. Review.
Cited by
-
Probing the nature of black holes: Deep in the mHz gravitational-wave sky.Exp Astron (Dordr). 2021;51(3):1385-1416. doi: 10.1007/s10686-021-09741-9. Epub 2021 Sep 3. Exp Astron (Dordr). 2021. PMID: 34720415 Free PMC article.
-
Exploring New Physics Frontiers Through Numerical Relativity.Living Rev Relativ. 2015;18(1):1. doi: 10.1007/lrr-2015-1. Epub 2015 Sep 21. Living Rev Relativ. 2015. PMID: 28179851 Free PMC article. Review.
-
Optical analogues of the Newton-Schrödinger equation and boson star evolution.Nat Commun. 2016 Nov 14;7:13492. doi: 10.1038/ncomms13492. Nat Commun. 2016. PMID: 27841261 Free PMC article.
References
-
- Adam C, Grandi N, Klimas P, Sánchez-Guillén J, Wereszczyński A. Compact boson stars in K field theories. Gen. Relativ. Gravit. 2010;42:2663–2701. doi: 10.1007/s10714-010-1006-4. - DOI
-
- Agnihotri P, Schaffner-Bielich J, Mishustin IN. Boson stars with repulsive self-interactions. Phys. Rev. D. 2009;79:084033. doi: 10.1103/PhysRevD.79.084033. - DOI
-
- Akhoury, R. and Gauthier, C.S., “Galactic Halos and Black Holes in Non-Canonical Scalar Field Theories”, arXiv, e-print, (2008). [ADS], [arXiv:0804.3437 [hep-th]]. (Cited on page 17.)
-
- Alcubierre M. Introduction to 3+1 Numerical Relativity. Oxford; New York: Oxford University Press; 2008.
-
- Alcubierre M, Becerril R, Guzmán FS, Matos T, Núñez D, Ureña-López LA. Numerical studies of Φ2-oscillatons. Class. Quantum Grav. 2003;20:2883–2903. doi: 10.1088/0264-9381/20/13/332. - DOI
Publication types
LinkOut - more resources
Full Text Sources
