A synthesis of the basal thermal state of the Greenland Ice Sheet

Abstract

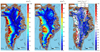
The basal thermal state of an ice sheet (frozen or thawed) is an important control upon its evolution, dynamics and response to external forcings. However, this state can only be observed directly within sparse boreholes or inferred conclusively from the presence of subglacial lakes. Here we synthesize spatially extensive inferences of the basal thermal state of the Greenland Ice Sheet to better constrain this state. Existing inferences include outputs from the eight thermomechanical ice-flow models included in the SeaRISE effort. New remote-sensing inferences of the basal thermal state are derived from Holocene radiostratigraphy, modern surface velocity and MODIS imagery. Both thermomechanical modeling and remote inferences generally agree that the Northeast Greenland Ice Stream and large portions of the southwestern ice-drainage systems are thawed at the bed, whereas the bed beneath the central ice divides, particularly their west-facing slopes, is frozen. Elsewhere, there is poor agreement regarding the basal thermal state. Both models and remote inferences rarely represent the borehole-observed basal thermal state accurately near NorthGRIP and DYE-3. This synthesis identifies a large portion of the Greenland Ice Sheet (about one third by area) where additional observations would most improve knowledge of its overall basal thermal state.

Figure 1

(a) Map of Greenland showing the spatial coverage of 1993–2013 radar-sounding data used in this study (same as MacGregor et al. [2015a]), the basal thermal state of deep boreholes and the locations of known subglacial lakes. Table 1 lists the sources for the borehole data and subglacial lake locations. (b) Ice-drainage systems (IDS) of the GrIS, as delineated and labeled by Zwally et al. [2012], overlain on the driving stress τ_d.

Figure 2

Schematic of Nye + melt (red) and Dansgaard–Johnsen (blue) 1-D ice-flow models in terms of their relative depth profiles (normalized by ice thickness H) of (a) horizontal velocity, (b) vertical velocity and (c) age. The underlying physical assumptions regarding the depth profiles of horizontal velocity for each model lead to the depth–age relationships shown. This latter modeled quantity (age) is that which we compare to observations (dated radiostratigraphy) to then infer the basal melt rate (ṁ) and shear layer thickness (h). In this schematic, age is normalized by its value at H − h in the Dansgaard–Johnsen model.

Figure 3

Modeled pressure-melting-corrected basal temperature across the GrIS $(T_{\mathit{\text{bed}}}^{\prime })$ from the end of the SeaRISE control-run experiments. The CISM, ISSM and PISM instances (panels b, e, and g; model names italicized) are improved relative to those included in the SeaRISE effort. Models with blue titles were initialized using various paleoclimatic forcings, whereas models with red titles assimilated modern data to determine their geometry and dynamics. The IcIES model is also slightly revised from that used in the SeaRISE experiments, and the AIF model uses a cubic exponent for the power-law relationship between basal motion and friction. White contours represent where $T_{\mathit{\text{bed}}}^{\prime }=-0.05°\mathrm{C}$, the temperature cut-off above which we assume the bed is thawed (Table 2).

Figure 4

Agreement in $T_{\mathit{\text{bed}}}^{\prime }$ between the SeaRISE control-run experiments and updated models shown in Figure 3, assuming that the bed is thawed if a model reports $T_{\mathit{\text{bed}}}^{\prime }\ge -0.05°\mathrm{C}$.

Figure 5

(a–c) Along-track and (d–f) gridded apparent basal melt rate ṁ (ice-equivalent), basal shear layer thickness h and shape factor φ across the GrIS, respectively. The first of these quantities was derived using the Nye + melt model (Equation 1), whereas the second two were derived using the Dansgaard–Johnsen model (Equation 4). Magenta line represents outermost limit of acceptability of 1-D ice-flow modeling for ≤9-ka-old radiostratigraphy [MacGregor et al., 2016]. Black outline in (b) and white outline in (d) represent ṁ = 0 and h = 0 contours, respectively. In (f), white (gray) solid line is φ = 1 (0.8) contour. Confidence regions for these outlines, based on gridding of the 95% confidence bounds for along-track values, have similar extents. Green boxes in (a) outline regions shown in Figure 6.

Figure 6

Along-track (a–c) basal melt rate ṁ, (d–f) basal shear layer thickness h and (g–i) shape factor φ in the (a,d,g) NW, (b,e,h) NEGIS and (c,f,i) SW regions, respectively. Background gray scale is observed surface speed. White lines are ice-drainage divides and magenta line is downstream limit of reliable 1-D modeling.

Figure 7

(a) Histogram of along-track and gridded shape factor φ values (Figure 5c,f), overlain on the qualitative physical interpretation of φ values. Note that the extent of these values does not typically reach the ice-sheet margin and includes ice divides. The small peak at φ = 0.5 for the along-track values is an anomaly associated with the optimization method that can lead to h = H (Equation 5). (b) Comparison between borehole-observed and radiostratigraphy-inferred φ values from radar transects that pass within 3 km of the boreholes. For boreholes with multiple radiostratigraphy-inferred estimates of φ, the standard deviation is also shown using error bars.

Figure 8

(a) Observed surface speed (u_s) across the GrIS [Joughin et al., 2010], filtered following MacGregor et al. [2016]. (b) Modeled ice-deformation speed at surface (u_def) assuming an entirely temperate ice column (Ā = 2.4 × 10⁻²⁴ Pa⁻³ s⁻¹; Equation 6). (c) Ratio of observed to modeled surface speed (u_s/u_def). Bold contours represent u_s/u_def = 1 considering both the standard values shown in (a) and (b) and uncertainty in both quantities.

Figure 9

Delineated onset of surface undulations across the GrIS. Green and red lines represent standard and conservative estimates of the location of the onset of surface undulations, respectively. Panels (b–d) shows zoomed-in versions of the boxes identified in (a) at the same scale, which is given in (c). Zoomed-in regions are the same as Figure 6.

Figure 10

(a) Outlines of boundaries between a frozen and thawed GrIS bed for the four methods considered in this study (§2.1–2.3; Figures 4, 5f, 8c and 9). For the 3-D models, the outline of their agreement denotes where more than half of the SeaRISE models agree that the bed is thawed, based on their synthesis (Figure 4). (b) Agreement between the four methods (S) regarding the basal thermal state. (c) Cold- and warm-bias agreement (S_cold and S_warm, respectively) determined using each method’s confidence bounds or uncertainty estimates. Because only two applied methods constrain where the bed is frozen (3-D models and φ), but all four constrain where it is thawed, the range of S is +2 frozen to +4 (all) thawed.

Figure 11

Likely basal thermal state of the GrIS (L), based on where the standard, cold- and warm-bias estimates of this state agree (Figure 10b–d; §2.4; Table 3). The white line represents where the 1979–2014 mean surface mass balance is zero, i.e., the approximate equilibrium line, as modeled by the Modèle Atmosphérique Régionale (MAR v3.5.2; Fettweis [2007]).

Figure 12

(right y-axis; lines) Areal distributions of readily observed or inferred GrIS properties as a function of likely basal thermal state (L ; Figure 11). (left y-axis; background fill) Relative fraction of the three possible values of L (likely frozen, uncertain or likely thawed) contained within each bin. (a) Surface elevation and (b) slope are derived from GIMP [Howat et al., 2014], (c) ice thickness from Morlighem et al. [2014], (d) driving stress from Figure 1b, (e) surface speed from Figure 8a and (f) surface mass balance from MAR (same as in Figure 11).