Onset of mortality increase with age and age trajectories of mortality from all diseases in the four Nordic countries

Abstract

Background: The answer to the question "At what age does aging begin?" is tightly related to the question "Where is the onset of mortality increase with age?" Age affects mortality rates from all diseases differently than it affects mortality rates from nonbiological causes. Mortality increase with age in adult populations has been modeled by many authors, and little attention has been given to mortality decrease with age after birth.

Materials and methods: Nonbiological causes are excluded, and the category "all diseases" is studied. It is analyzed in Denmark, Finland, Norway, and Sweden during the period 1994-2011, and all possible models are screened. Age trajectories of mortality are analyzed separately: before the age category where mortality reaches its minimal value and after the age category.

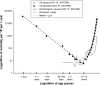
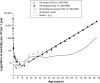
Results: Resulting age trajectories from all diseases showed a strong minimum, which was hidden in total mortality. The inverse proportion between mortality and age fitted in 54 of 58 cases before mortality minimum. The Gompertz model with two parameters fitted as mortality increased with age in 17 of 58 cases after mortality minimum, and the Gompertz model with a small positive quadratic term fitted data in the remaining 41 cases. The mean age where mortality reached minimal value was 8 (95% confidence interval 7.05-8.95) years. The figures depict an age where the human population has a minimal risk of death from biological causes.

Conclusion: Inverse proportion and the Gompertz model fitted data on both sides of the mortality minimum, and three parameters determined the shape of the age-mortality trajectory. Life expectancy should be determined by the two standard Gompertz parameters and also by the single parameter in the model c/x. All-disease mortality represents an alternative tool to study the impact of age. All results are based on published data.

Keywords: Nordic countries; age; all diseases; external causes; mortality.

Figure 1

Age trajectories of mortality in Norway in the log–log scale in 1996.

Figure 2

Age trajectories of mortality in Norway in the semilogarithmic scale in 1996.

Figure 3

Age trajectory of all-disease mortality fitted by the two models in Denmark in the log–log scale in 1994.

Figure 4

Age trajectory of all-disease mortality fitted by the two models in Denmark in the semilogarithmic scale in 1994.

Figure 5

Age trajectories of all-disease mortality in the age interval 0–10 years fitted by the four models using least squares in the log–log scale.