The Motion of Point Particles in Curved Spacetime

Abstract

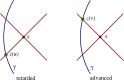
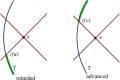
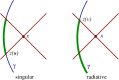
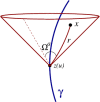
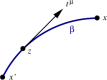
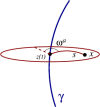
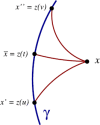
This review is concerned with the motion of a point scalar charge, a point electric charge, and a point mass in a specified background spacetime. In each of the three cases the particle produces a field that behaves as outgoing radiation in the wave zone, and therefore removes energy from the particle. In the near zone the field acts on the particle and gives rise to a self-force that prevents the particle from moving on a geodesic of the background spacetime. The self-force contains both conservative and dissipative terms, and the latter are responsible for the radiation reaction. The work done by the self-force matches the energy radiated away by the particle. The field's action on the particle is difficult to calculate because of its singular nature: The field diverges at the position of the particle. But it is possible to isolate the field's singular part and show that it exerts no force on the particle - its only effect is to contribute to the particle's inertia. What remains after subtraction is a smooth field that is fully responsible for the self-force. Because this field satisfies a homogeneous wave equation, it can be thought of as a free (radiative) field that interacts with the particle; it is this interaction that gives rise to the self-force. The mathematical tools required to derive the equations of motion of a point scalar charge, a point electric charge, and a point mass in a specified background spacetime are developed here from scratch. The review begins with a discussion of the basic theory of bitensors (Section 2). It then applies the theory to the construction of convenient coordinate systems to chart a neighbourhood of the particle's word line (Section 3). It continues with a thorough discussion of Green's functions in curved spacetime (Section 4). The review concludes with a detailed derivation of each of the three equations of motion (Section 5).

Figure 1

In flat spacetime, the retarded potential at x depends on the particle’s state of motion at the retarded point z(u) on the world line; the advanced potential depends on the state of motion at the advanced point z(v).

Figure 2

In curved spacetime, the retarded potential at x depends on the particle’s history before the retarded time u; the advanced potential depends on the particle’s history after the advanced time υ.

Figure 3

In curved spacetime, the singular potential at x depends on the particle’s history during the interval u ≤ τ ≤ v; for the radiative potential the relevant interval is −∞ < τ ≤ v.

Figure 4

Retarded coordinates of a point x relative to a world line γ. The retarded time u selects a particular null cone, the unit vector selects a particular generator of this null cone, and the retarded distance r selects a particular point on this generator.

Figure 5

The base point x′, the field point x, and the geodesic β that links them. The geodesic is described by parametric relations z^μ(λ), and t^μ = dz^μ/dλ is its tangent vector.

Figure 6

Fermi normal coordinates of a point x relative to a world line γ. The time coordinate t selects a particular point on the word line, and the disk represents the set of spacelike geodesics that intersect γ orthogonally at z(t). The unit vector selects a particular geodesic among this set, and the spatial distance s selects a particular point on this geodesic.

Figure 7

Retarded coordinates ofa point x relative to a world line γ. The retarded time u selects a particular null cone, the unit vector selects a particular generator of this null cone, and the retarded distance r selects a particular point on this generator. This figure is identical to Figure 4.

Figure 8

The retarded, simultaneous, and advanced points on a world line γ. The retarded point x′ ≡ z(u) is linked to x by a future-directed null geodesic. The simultaneous point is linked to x by a spacelike geodesic that intersects γ orthogonally. The advanced point x″ = is linked to x by a past-directed null geodesic.

Figure 9

The region within the dashed boundary represents the normal convex neighbourhood of the point x. The world line γ enters the neighbourhood at proper time τ_< and exits at proper time τ_>. Also shown are the retarded point z(u) and the advanced point z(v).

Figure 10

A black hole, represented by the black disk, is immersed in a background spacetime. The internal zone extends from r = 0 to , while the external zone extends from r = r_e ≫ m to r = ∞. When there exists a buffer zone that extends from r = r_e to r = r_i. In the buffer zone m/r and are both small.