Magnetism and local symmetry breaking in a Mott insulator with strong spin orbit interactions
- PMID: 28181502
- PMCID: PMC5309813
- DOI: 10.1038/ncomms14407
Magnetism and local symmetry breaking in a Mott insulator with strong spin orbit interactions
Abstract
Study of the combined effects of strong electronic correlations with spin-orbit coupling (SOC) represents a central issue in quantum materials research. Predicting emergent properties represents a huge theoretical problem since the presence of SOC implies that the spin is not a good quantum number. Existing theories propose the emergence of a multitude of exotic quantum phases, distinguishable by either local point symmetry breaking or local spin expectation values, even in materials with simple cubic crystal structure such as Ba2NaOsO6. Experimental tests of these theories by local probes are highly sought for. Our local measurements designed to concurrently probe spin and orbital/lattice degrees of freedom of Ba2NaOsO6 provide such tests. Here we show that a canted ferromagnetic phase which is preceded by local point symmetry breaking is stabilized at low temperatures, as predicted by quantum theories involving multipolar spin interactions.
Conflict of interest statement
The authors declare no competing financial interests.
Figures
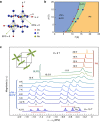

 0) plane of the crystal which contains three high symmetry directions: [001], [111] and [110]. (b) The mean peak-to-peak splitting (δq) between any two adjacent peaks of the triplets I and II. Error bars reflect the scattering of deduced (δq) values. Solid line is the fit to
0) plane of the crystal which contains three high symmetry directions: [001], [111] and [110]. (b) The mean peak-to-peak splitting (δq) between any two adjacent peaks of the triplets I and II. Error bars reflect the scattering of deduced (δq) values. Solid line is the fit to  , where θ denotes the angle between the principal axis of the EFG (Vzz) and the applied magnetic field (H) as depicted for nuclei with spin I=3/2 and magnetic moment μ (see Supplementary Note 5). (c) Schematic of a proposed lattice distortion involving the O2− ions. The distortion breaks cubic symmetry at the Na site giving rise to finite electric field gradient (EFG). Different types and colours of double arrows illustrate unequal magnitude of oxygen displacements. Displacements along different axes can comprise either from compression or elongation of the oxygen bonds (see Supplementary Note 5). Depicted distortion magnitude is not to scale with the distance between nearest neighbour Os atoms, and is amplified for clarity. (d) Schematic of the energy levels of a spin-3/2 nucleus in a finite magnetic field and in the presence of quadrupolar interaction with EFG, generated by surrounding electronic charges, and resulting NMR spectra. In the absence of quadrupolar interaction spectrum consists of a single narrow line at frequency ω and of width Δω. In the presence of quadrupolar interaction, the centre transition remains at frequency ω, while the satellite transitions appear at frequencies shift by ±δq , proportional to the magnitude of the EFG. For small values of the EFG, satellite transition cannot be resolved and only line broadening is observed. Strictly speaking, there is also a broadening due to the distribution of magnitude of the EFG itself, but this is manifested only on the satellites and not on the central transition. In our case, this distribution can be neglected as all the lines show the same width.
, where θ denotes the angle between the principal axis of the EFG (Vzz) and the applied magnetic field (H) as depicted for nuclei with spin I=3/2 and magnetic moment μ (see Supplementary Note 5). (c) Schematic of a proposed lattice distortion involving the O2− ions. The distortion breaks cubic symmetry at the Na site giving rise to finite electric field gradient (EFG). Different types and colours of double arrows illustrate unequal magnitude of oxygen displacements. Displacements along different axes can comprise either from compression or elongation of the oxygen bonds (see Supplementary Note 5). Depicted distortion magnitude is not to scale with the distance between nearest neighbour Os atoms, and is amplified for clarity. (d) Schematic of the energy levels of a spin-3/2 nucleus in a finite magnetic field and in the presence of quadrupolar interaction with EFG, generated by surrounding electronic charges, and resulting NMR spectra. In the absence of quadrupolar interaction spectrum consists of a single narrow line at frequency ω and of width Δω. In the presence of quadrupolar interaction, the centre transition remains at frequency ω, while the satellite transitions appear at frequencies shift by ±δq , proportional to the magnitude of the EFG. For small values of the EFG, satellite transition cannot be resolved and only line broadening is observed. Strictly speaking, there is also a broadening due to the distribution of magnitude of the EFG itself, but this is manifested only on the satellites and not on the central transition. In our case, this distribution can be neglected as all the lines show the same width.
 . Typical error bars are on the order of a few per cent and not shown for clarity. Lines are guide to the eyes.
. Typical error bars are on the order of a few per cent and not shown for clarity. Lines are guide to the eyes.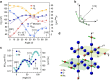
References
-
- Chen G., Balents L. & Schnyder A. P. Spin-orbital singlet and quantum critical point on the diamond lattice: FeSc2S4. Phys. Rev. Lett. 102, 096406 (2009). - PubMed
-
- Jackeli G. & Khaliullin G. Mott insulators in the strong spin-orbit coupling limit: from heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009). - PubMed
-
- Chen G., Pereira R. & Balents L. Exotic phases induced by strong spin-orbit coupling in ordered double perovskites. Phys. Rev. B 82, 174440 (2010).
-
- Chen G. & Balents L. Spin-orbit coupling in d2 ordered double perovskites. Phys. Rev. B 84, 094420 (2011).
-
- Pesin D. & Balents L. Mott physics and band topology in materials with strong spin-orbit interaction. Nat. Phys. 6, 376–381 (2010).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

