Multivariate meta-analysis with an increasing number of parameters

Abstract

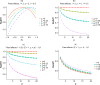
Meta-analysis can average estimates of multiple parameters, such as a treatment's effect on multiple outcomes, across studies. Univariate meta-analysis (UVMA) considers each parameter individually, while multivariate meta-analysis (MVMA) considers the parameters jointly and accounts for the correlation between their estimates. The performance of MVMA and UVMA has been extensively compared in scenarios with two parameters. Our objective is to compare the performance of MVMA and UVMA as the number of parameters, p, increases. Specifically, we show that (i) for fixed-effect (FE) meta-analysis, the benefit from using MVMA can substantially increase as p increases; (ii) for random effects (RE) meta-analysis, the benefit from MVMA can increase as p increases, but the potential improvement is modest in the presence of high between-study variability and the actual improvement is further reduced by the need to estimate an increasingly large between study covariance matrix; and (iii) when there is little to no between-study variability, the loss of efficiency due to choosing RE MVMA over FE MVMA increases as p increases. We demonstrate these three features through theory, simulation, and a meta-analysis of risk factors for non-Hodgkin lymphoma.

Keywords: Efficiency; Fixed-effect models; Multivariate meta-analysis; Random effects models.

Fig. 1

The relative efficiency (RelEff) compares the performance of MVMA and UVMA for FE meta-analysis when the covariance matrix is exchangeable. The RelEff (1) decreases as the difference between the within-study correlations increases (2) decreases as the number of parameters increases and (3) decreases as the number of studies increases. (a) A two-study, two parameter example illustrating (1). (b) A two-study, multi-parameter example illustrating (1) and (2). (c) A twenty-study, multi-parameter example illustrating (1) and (2). (d) A multi-study, multi-parameter example illustrating (1), (2), and (3). The notation includes I: number of studies, p: number of parameters, $S_i^2$: within-study variance of an estimated parameter in study i, ρ_i: within-study correlation between two estimated parameters in study i, and $r=S_1^2/(S_1^2+S_2^2)$.

Fig. 2

The relative efficiency when the between-study covariance matrices are known (RelEff^T) and when the between-study covariance matrices are unknown (RelEff) compares the performance of MVMA and UVMA for RE meta-analyses when the covariance matrices are exchangeable. Properties of RelEff^T and RelEff include (1) RelEff^T is less than RelEff (2) RelEff^T and RelEff both decrease as the number of parameters increases (3) RelEff^T and RelEff both decrease as the between-study variance decreases (4) the difference between RelEff^T and RelEff decreases as the number of studies increases. (a) A twenty-study, multi-parameter example illustrating (1), (2), and (3). (b) A multi-study, multi-parameter example illustrating (1), (2), and (4). The notation includes I: number of studies, p: number of parameters, $S_i^2$: within-study variance of an estimated parameter in study i, σ²: between-study variance of a single parameter, Σ: between-study covariance matrix, ρ_i: within-study correlation between two estimated parameters in study i, ρ^BS: between-study correlation between two parameters.