Modeling the two-way feedback between contractility and matrix realignment reveals a nonlinear mode of cancer cell invasion

Abstract

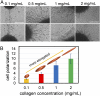
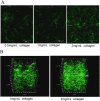
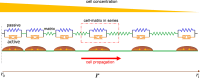
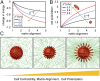
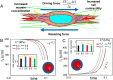
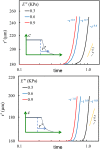
Cancer cell invasion from primary tumors is mediated by a complex interplay between cellular adhesions, actomyosin-driven contractility, and the physical characteristics of the extracellular matrix (ECM). Here, we incorporate a mechanochemical free-energy-based approach to elucidate how the two-way feedback loop between cell contractility (induced by the activity of chemomechanical interactions such as Ca²⁺ and Rho signaling pathways) and matrix fiber realignment and strain stiffening enables the cells to polarize and develop contractile forces to break free from the tumor spheroids and invade into the ECM. Interestingly, through this computational model, we are able to identify a critical stiffness that is required by the matrix to break intercellular adhesions and initiate cell invasion. Also, by considering the kinetics of the cell movement, our model predicts a biphasic invasiveness with respect to the stiffness of the matrix. These predictions are validated by analyzing the invasion of melanoma cells in collagen matrices of varying concentration. Our model also predicts a positive correlation between the elongated morphology of the invading cells and the alignment of fibers in the matrix, suggesting that cell polarization is directly proportional to the stiffness and alignment of the matrix. In contrast, cells in nonfibrous matrices are found to be rounded and not polarized, underscoring the key role played by the nonlinear mechanics of fibrous matrices. Importantly, our model shows that mechanical principles mediated by the contractility of the cells and the nonlinearity of the ECM behavior play a crucial role in determining the phenotype of the cell invasion.

Keywords: Rho pathway; cell contractility; cell invasion; fibrous matrices; matrix realignment.

Fig. 1.

Cell polarization increases with collagen concentration. (A) Melanoma cells invading collagen matrices exhibit strong polarization, which increases with the concentration of collagen. (Scale bars: 100 µm.) (B) The elongation of cells (ratio of the major to the minor axes of the cells) increases with collagen concentration.

Fig. S1.

The (A) 2D and (B) 3D images of collagen fibers adjacent to the spheroids of tumor cells show that, at higher concentrations of collagen (1.0 and 2.0 mg/mL), there is an increase in the density of the fibers and the cross-links of the matrix. Collagen concentrations lower than 1.0 mg/mL could not be imaged due to the loose, flimsy nature of the matrix, which caused significant blurring of the image.

Fig. S2.

Comparison between the mitomycin C-treated cells and vehicle cells invading collagen matrix. Mitomycin C does not appear to affect the rate of invasion of melanoma cells, demonstrating that, at these time points, the spread of cells is due largely to invasion, and not cell proliferation.

Fig. 2.

Model of cell invasion from a tumor spheroid into a fibrous matrix. (A) The total free energy (U_total) of cells within a tumor spheroid embedded in a matrix is a function of the chemomechanical energy of the cells (U_cell), the mechanical energy of the matrix (U_matrix), and the adhesion energy associated with cellular adhesions (U_adhesion). The Ca²⁺ pathway and the Rho pathway, which affect cell contractility and the ability of cells to move through a matrix, are implemented in our model. (B) Realignment of the matrix fibers in response to the contractility of the cells. The red curve shows the radial stress, and the blue curve shows the magnitude of the transverse stress (without the negative sign). Radial and transverse directions are shown in the matrix. The stiffness of the matrix in the radial and transverse directions are denoted $E_r^m$ and $E_{\theta }^m$, respectively. (C) The concentration profile of the cells, c(r), as a function of the distance from the center of the cluster, r. The initial radius, R, is marked by the dashed line. For the invasive cluster, three regions are defined: cluster (r < r₀), invaded region (r₀ < r < r₁), and the matrix (r₁ < r). The parameter λ governs the extent of the invaded region in such a way that, with increasing λ the size of the invaded region increases.

Fig. S3.

Radial displacement field in the matrix surrounding a cell spheroid. Displacement decays rapidly in randomly oriented matrices, whereas the displacement field is long-ranged in the aligned matrices. We have used the parameters $r_0=0.75R$ and $\lambda =1$. Also, $E_r^m/E_{\theta }^m=1$ and $E_r^m/E_{\theta }^m=4$ in the random and aligned matrices, respectively.

Fig. S4.

The arrangement of the contractile cells and the matrix elements in the invaded region. The cell–matrix representative unit cell is shown. Cell element is composed of the active and passive parts and is placed “in series” with the matrix element. Cell concentration decays gradually along the radial direction and reaches zero at $r=r_1$.

Fig. 3.

The two-way feedback loop between cell contractility and matrix fiber realignment. (A) As the cells align the fibers, up-regulation in the recruitment of myosin motors that follows leads to a reduction in the total free energy of the system. (B) Meanwhile, the cells adopt a polarized morphology in proportion to the stiffness of the matrix. The green arrow shows that, with increasing elastic modulus of the matrix (E^m), the polarization increases. (C) Schematic showing the direct reciprocity between fiber alignment and cell polarization. r₀ = 0.75R and λ = 1 in all figures. Fiber alignment is calculated from $E_r^m$ = $E_{\theta }^m$ and cell polarization is ρ_rr/ρ_θθ. Energies are normalized with respect to the energy of E^m = 0.3 kPa when $E_r^m$/$E_{\theta }^m$ = 1.

Fig. 4.

Cell contractility and matrix realignment increase cell polarization of invading cells. (A) Polarization of the cells located at (r) as the function of the elastic modulus of the matrix. Cells inside the cluster (r < r₀) are not polarized (ρ_rr/ρ_θθ = 1). Cells in the invaded region (r > r₀) are highly polarized (ρ_rr/ρ_θθ > 1). The green arrow shows that the polarization increases with the stiffness of the matrix (E^m). Note that, within the invaded region, the polarization decays with the distance from the spheroid. The top and the bottom rows correspond to two different time instances of the cell invasion. The current radius of the spheroid (r₀) is r₀ = 0.75R and r₀ = 0.65R in the top and bottom rows, respectively. These results show that the cell polarization (or elongation) is increasing with the progression of the cell invasion. (B) Matrix realignment also increases with time, suggesting that cell polarization is directly proportional to the matrix realignment. Matrix alignment is determined from the ratio of the matrix elastic moduli in the radial and transverse directions. Also, λ = 1 in all of the figures.

Fig. 5.

Biphasic effect of matrix concentration on cell invasion. (A) Change in the total free energy of the system (ΔU_total) as a function of the radius of the spheroid (r₀) and the parameter that governs the extent of the invaded region (λ). The elastic modulus of the surrounding matrix is varied between 0.02 and 0.60 kPa. The change in the energy is normalized with respect to the initial energy of the system (at r₀ = R, λ = 0). The metastatic pathway starting from the full spheroid is also shown (green arrow line connecting the origin to an arbitrary point shown by the yellow cross). In the absence of cell contractility or for the spheroid placed in the soft matrix (0.02 kPa), cell invasion is accompanied by an increase in the free energy. Alternatively, increasing the matrix stiffness beyond the critical stiffness (0.15 kPa) leads to the reduction of the energy and spontaneous invasion of the cells. (B) Increasing ligand density decreases the matrix critical elastic modulus (blue line). (C) At the concentration of collagen beyond the critical value (0.5 mg/mL), melanoma cells leave the cluster and invade into the 3D collagen matrix. (Scale bars: 500 µm.) The tangent elastic modulus between 3 and 7% axial strains (∼0.16 to ∼0.75 kPa) at 0.5, 1.0, and 2.0 mg/mL collagen concentrations is also shown from ref. . (D) Quantitative analysis of the melanoma cell invasion shows a biphasic response to the concentration of collagen. **P < 0.0018, ***P < 0.0009, and ****P < 0.0001. (E and F) Three-dimensional imaging of the tumor cells leaving the spheroid and invading the surrounding matrix with (E) 1.0 mg/mL and (F) 2.0 mg/mL collagen. Cells (red) are aligned with collagen fibers (green) in the radial direction, perpendicular to the boundary of the spheroid (blue dashed line). At 1 mg/mL collagen, cells invade rapidly away from the sphere, whereas at 2 mg/mL collagen, cells are located closer to the spheroid.

Fig. S5.

Biphasic invasive behavior of cells does not change in the presence of MMP inhibitors. (A) Quantification of invasion of 1205Lu melanoma cells, treated with 500 nM MMP2/9 inhibitor, from a 3D spheroid into a fibrous matrix of increasing collagen concentration. (B) Quantification of invasion of 1205Lu melanoma cells, treated with 1 μM MMP2/9 inhibitor, from a 3D spheroid into a fibrous matrix of increasing collagen concentration. ****P < 0.0001; **P < 0.007.

Fig. S6.

(A) Treating the cells with the Rho inhibitor, Y27632, leads to lower levels of cell invasion. In the presence of the Rho inhibitor, Y27632, invasion of melanoma cells in the two concentrations of collagen that are the most invasive (0.5 and 1 mg/mL) is inhibited. (**P < 0.0018, ***P < 0.0009.) (B) In agreement with the experiment, by inhibiting the molecular pathways such as Ca²⁺ and Rho in our model, cell invasion leads to an increase in free energy, and therefore invasion is less favorable. The change in the energy is normalized with respect to the initial energy of the system (at $r_0=r_1=R$).

Fig. 6.

The kinetics of the cell invasion as a function of the matrix stiffness. (A) Schematic showing the dynamics of the forces involved in cell invasion. The driving force from cell contractility has to overcome the forces resisting cell movement, leading to the invasion of the cells into the matrix. (B) The shrinking of the spheroid radius r₀ and (C) the advance of the front line r₁ as the function of the matrix elastic modulus and time. The rate of the cell invasion shows the biphasic behavior in response to the stiffness of the matrix. Also, the metastatic cell migration predicted by our model follows superdiffusive behavior (with the exponent larger than 0.5). Time is normalized by multiplying by M U_total(r₀ = r₁ = R, E^m = 0.3 kPa)/R².

Fig. S7.

The biphasic response of the cell invasion to the stiffness of the surrounding matrix predicted by our model.

Fig. S8.

The movement of two tracers initially located at $r^{\ast }/R=0.9$ (Top) and $r^{\ast }/R=0.8$ (Bottom) in the matrix with normalized time. Tracers leave the cluster as they become exposed to the matrix. The propagation of the tracers in the matrix follows the superdiffusive behavior, indicating that the cell migration process is directed under the driving force generated by the matrix.

Fig. S9.

Effect of the matrix critical strain and strain stiffening on cell polarization and matrix alignment. (A) Decreasing the matrix critical strain (ε_cr) and (B) matrix strain stiffening (n) increases the matrix fiber realignment and cell polarization. This is consistent with cells cultured in nonfibrous matrices such as BME (n = 0), adopting a more rounded morphology. E^m = 0.6 kPa, r₀ = 0.75R, and λ = 1 in all figures.