Cellular Hierarchy as a Determinant of Tumor Sensitivity to Chemotherapy

Abstract

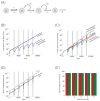
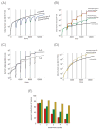
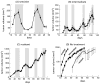
Chemotherapy has been shown to enrich cancer stem cells in tumors. Recently, we demonstrated that administration of chemotherapy to human bladder cancer xenografts could trigger a wound-healing response that mobilizes quiescent tumor stem cells into active proliferation. This phenomenon leads to a loss of sensitivity to chemotherapy partly due to an increase in the number of tumor stem cells, which typically respond to chemotherapy-induced cell death less than more differentiated cells. Different bladder cancer xenografts, however, demonstrate differential sensitivities to chemotherapy, the basis of which is not understood. Using mathematical models, we show that characteristics of the tumor cell hierarchy can be crucial for determining the sensitivity of tumors to drug therapy, under the assumption that stem cell enrichment is the primary basis for drug resistance. Intriguingly, our model predicts a weaker response to therapy if there is negative feedback from differentiated tumor cells that inhibits the rate of tumor stem cell division. If this negative feedback is less pronounced, the treatment response is predicted to be enhanced. The reason is that negative feedback on the rate of tumor cell division promotes a permanent rise of the tumor stem cell population over time, both in the absence of treatment and even more so during drug therapy. Model application to data from chemotherapy-treated patient-derived xenografts indicates support for model predictions. These findings call for further research into feedback mechanisms that might remain active in cancers and potentially highlight the presence of feedback as an indication to combine chemotherapy with approaches that limit the process of tumor stem cell enrichment. Cancer Res; 77(9); 2231-41. ©2017 AACR.

Figure 1

(A) Schematic representation of tumor dynamics without treatment (no negative feedback). Quiescent stem cells, Q, actively proliferating stem cells, S, transit amplifying cells, T, and differentiated cells, D. For explanation, see text. Treatment dynamics without negative feedback according to model (1). (B) Tumor treatment dynamics assuming that the treatment induced death rate of tumor stem cells is more pronounced that the treatment-induced stem cell expansion. Five treatment cycles are shown, indicated in grey. The black line is the untreated control, the blue line the chemotherapy-treated simulation. (C) Tumor treatment dynamics, assuming that the treatment-induced tumor stem cell expansion is more pronounced than the stem cell death rate during therapy. The black line shows the untreated control, the red line shows the chemotherapy-treated simulation, and the green line shows the same in the absence of a wound-healing response, corresponding to celecoxib administration. (D) Treatment dynamics showing the population of tumor stem cells (Q+S, solid line) and more differentiated cells (T+D, dashed line), based on the red line in panel C. (E) Percent of tumor reduction during each treatment cycle. This is shown for the simulations in panel C: in the presence (red) and absence (green) of the wound-healing response. Parameters were chosen as follows: r₁=0.02; r₂=0.05; p₁=0.6; p₂=0.45; δ=0.0025; f=0.005; g=0.001; α=1; ε=1; η=1; c₁=1; c₂=1. For (B) c₃=0.02 and β=0.001. For (C–E): c₃=0.002. For simulations with the wound-healing response, β=1. For simulations without a wound-healing response, β=0. Parameter values were chosen for the purpose of illustration, and time units are thus arbitrary. Timing and duration of treatment cycles was chosen to allow for the re-population of the more differentiated tumor cells from the tumor stem cells between treatments, which also applies to subsequent figures.

Figure 2

(A) Schematic representation of tumor dynamics (with negative feedback). The basic dynamics are the same as in Figure 1A. In addition, we model negative feedback from differentiated cells on the cell division rates of tumor stem cells and transit amplifying cells. (B) Negative feedback and its effect on tumor growth. The black line depicts tumor growth without of negative feedback, simulated by model (1). The green and red lines show tumor growth dynamics in the presence of weak and strong feedback, respectively. (C) When there is negative feedback, the stem cell fraction increases with tumor size (blue lines; Q+S dashed line, T+D solid line). When there is no feedback the stem cell fraction remains constant (black lines). Parameters were chosen as follows. In panel (A): r₁=0.02; r₂=0.05; p₁=0.7; p₂=0.45; δ=0.00025; f=0.005; g=0.001; α=1; ε=1; ε=1; h=0.01; β=c₁=c₂=c₃=0; for weak negative feedback, k=0.2; for strong negative feedback, k=1. For absence of feedback, h=0. For panel (C): k=0.3 and p=0.6 (all other parameters are the same as in (A); h=0 for no feedback).

Figure 3

Treatment dynamics in the presence of negative feedback on cell division in model (2). (A) Tumor treatment dynamics assuming that the treatment induced death rate of tumor stem cells is more pronounced that the treatment-induced stem cell expansion. Five treatment cycles are shown, indicated in grey. The black line is the untreated control, the blue line the chemotherapy-treated simulation. (B) Tumor treatment dynamics, assuming that the treatment-induced tumor stem cell expansion is more pronounced than the stem cell death rate during therapy. The black line shows the untreated control, the red line shows the chemotherapy-treated simulation, and the green line shows the same in the absence of a wound-healing response, corresponding to celecoxib administration. (C) Treatment dynamics showing the population of tumor stem cells (Q+S, solid line) and more differentiated cells (T+D, dashed line), based on the red line in panel B. (D) Same as panel (B), but with weaker feedback inhibition. Only the untreated simulation and the chemotherapy simulation in the presence of a wound-healing response are shown. (E) Percent of tumor reduction during each treatment cycles. The color codes correspond to the simulations shown in the corresponding colors in panels (B) and (D). Parameters were chosen as follows: r₁=0.02; r₂=0.05; p₁=0.7; p₂=0.45; δ=0.0025; f=0.005; g=0.001; α=1; ε=1; η=1; h=0.01; c₁=1; c₂=1, For (A) c₃=0.02, β=0.001, k=1. For (B–D): c₃=0.002. For simulations with the wound-healing response, β=1. For simulations without a wound-healing response, β=0. For stronger feedback, k=1; for weaker feedback, k=0.2.

Figure 4

Spatial dynamics. (A) Three dimensional representation of a tumor. (B) Cross section of a tumor 3D tumor. A large number of stem cells (blue and red) are “trapped” in the tumor mass where they are unable to divide. (C) A tumor during treatment. The killing of transit and differentiated cells frees up space, which allows formerly trapped stem cells to divide. (D) Tumor dynamics during three treatment cycles, indicated in grey. Red: intact wound-healing response. Green: No wound-healing response. Black: No treatment. (See Figure S2 for simulations where the treated tumor remains consistently smaller than the untreated tumor.) (E) Percent of tumor reduction during the three treatment cycles. (F) Fraction of stem cells in the tumor population (Q+S)/(Q+S+T+D) for the treated tumor with wound-healing response. Parameters were chosen as follows: r₁=r₂=10; p₁=0.55; p₂=0.45; δ=0.00025; f=0.1; g=0.01; α=1; ε=1; η=0.02; h=2; β=0.5; c₃=0.001. Panels A–C (weak feedback): c₁=c₂=20, k=0.2. Panels D–F (strong feedback): c₁=c₂=0.1, k=1.

Figure 5

Experimental data documenting treatment dynamics of patient-derived bladder cancer mouse xenografts (A–C), and the dynamics of tumor growth without treatment (D). The tumors were treated with the chemotherapy regime gemcitabine and cisplatin (GC), treatment cycles are indicated in grey. Xenografts from three patient-derived cell lines are shown and designated as “sensitive”, “intermediate”, and resistant, based on qualitative observations. The “resistant” cell line data are re-plotted from Kurtova et al. (10), the data for the “intermediate” and “sensitive” xenografts were collected in the context of the same study but have not been previously published. Details of the experimental designs and the number of repeats are given in Kurtova et al. (10).