Dueling biological and social contagions

Abstract

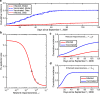
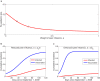
Numerous models explore how a wide variety of biological and social phenomena spread in social networks. However, these models implicitly assume that the spread of one phenomenon is not affected by the spread of another. Here, we develop a model of "dueling contagions", with a particular illustration of a situation where one is biological (influenza) and the other is social (flu vaccination). We apply the model to unique time series data collected during the 2009 H1N1 epidemic that includes information about vaccination, flu, and face-to-face social networks. The results show that well-connected individuals are more likely to get vaccinated, as are people who are exposed to friends who get vaccinated or are exposed to friends who get the flu. Our dueling contagion model suggests that other epidemiological models may be dramatically underestimating the R₀ of contagions. It also suggests that the rate of vaccination contagion may be even more important than the biological contagion in determining the course of the disease. These results suggest that real world and online platforms that make it easier to see when friends have been vaccinated (personalized vaccination campaigns) and when they get the flu (personalized flu warnings) could have a large impact on reducing the severity of epidemics. They also suggest possible benefits from understanding the coevolution of many kinds of dueling contagions.

Figure 1. Temporal dynamics of concurrent spreading of vaccination and flu in a real social network.

(a) Shows the cumulative incidence of vaccinated individuals and infected ones since September 1, 2009. The levels of vaccination coverage and of disease prevalence increase from zero and reach a plateau almost at the same time. These population aggregate behaviors offer a macroscopic view of the dueling contagions of vaccination and infection. (b–d) Display the snapshots of the social network at time point t = 10, 40, 120 days, respectively. Size of nodes is proportional to their network degree, and the color of nodes represents their health status: red infected, blue vaccinated and gray unvaccinated & healthy. These snapshots provide a microscopic, spatio-temporal view of the dueling contagions on the mapped friendship network, showing that the relatively fast spread of vaccination behavior impedes the development of a severe epidemic.

Figure 2. Social network degree as a determinant of vaccination.

The plot shows the average probability of subjects getting vaccinated, grouped by their network degree. The error bars denote one standard deviation of the estimated mean. This empirical observation validates a previous theoretical prediction: compared to periphery small-degree individuals, social hubs are more inclined to get vaccination possibly because of their increased chance of being exposed to others’ vaccination behavior as well as to the risk of infection.

Figure 3. Modeling “dueling contagions”.

(a) Shown are the real data regarding the population aggregate levels as in Fig. 1a (solid) and the best-fitting curves (dashed) using a simple dueling contagion model. Panel (b) shows the dependence of the epidemic size (t = 120) on the level of network responsiveness, ω, for other model parameters fixed with the estimated values. The circle marks the estimated value of ω₀. (c) and (d) Plotted are the predictions of population aggregate behaviors, based on the mean-field approximation of the dueling contagion processes, for a smaller ω = ω₀/2 (the triangle in panel b) and for a larger ω = 2ω₀ (the square in panel b), respectively. Our dataset allows us to infer the time scales that govern the dueling contagions of vaccination and infection: the estimated ω₀ ≈ 0.70 and R₀ ≈ 1.56. Intermediate values of ω induce simultaneous interdependence between vaccination and infection. On the other hand, extreme values of ω lead to time-scale separation in which one contagion dynamic is much faster or slower than the other. The health outcomes could be further improved if individuals more promptly had themselves vaccinated through social influence and/or in response to the epidemic: the epidemic size could be mitigated almost by half if the spread of vaccinating behavior was twice as fast. Model fitting results and simulations are based on the corse-grained version of the dueling contagion model, eqs (5–8).

Figure 4. Positive consequences of social contagion on public health.

Panel (a) depicts the final epidemic size (t = 120) as a function of the parameter a describing the extent of the role that social contagion, in comparison to the risk of infection, plays in an individual’s vaccination decision. The circle marks the estimated value of a₀ ≈ 0.24 inferred from our real data. Panels (b) and (c) plot the population aggregate levels of vaccination and infection, predicted by our dueling contagion model, with halving (a = a₀/2, the triangle in panel a) versus doubling (a = 2a₀, the square in panel a) the relative effect of peer influence on vaccinating decisions of individuals. It seems rational for one to decide whether or not to be vaccinated according to the level of disease prevalence, but paradoxically the health outcome is worsened, as self-interest and social optimum are at odds in this case. In contrast, herd behavior, induced by social influence, rapidly boosts the uptake level and thus most improves the health outcome: the epidemic size could be reduced by half if the spread of vaccination behavior is driven only by social contagion (a = 1). Simulated results are based on the corse-grained version of the dueling contagion model, eqs (5–8), using the best estimated values of the model parameters.