The effects of heat and mass diffusion on freely oscillating bubbles in a viscoelastic, tissue-like medium

Abstract

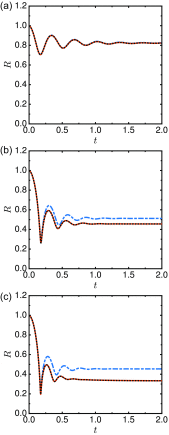
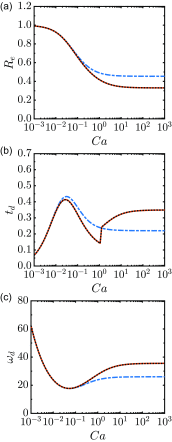
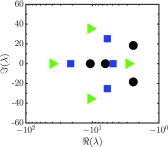
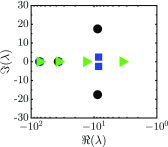
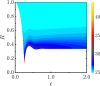
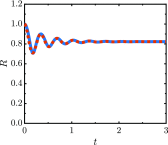
In certain cavitation-based ultrasound techniques, the relative importance of thermally vs mechanically induced damage is unclear. As a first step to investigate this matter, a numerical model for bubble dynamics in tissue-like, viscoelastic media is presented in which full thermal effects are included inside and outside the bubble, as well as interdiffusion of vapor and non-condensible gas inside the bubble. Soft tissue is assumed to behave according to a Kelvin-Voigt model in which viscous and elastic contributions are additive. A neo-Hookean formulation, appropriate for finite-strain elasticity, accounts for the large deformations produced by cavitation. Numerical solutions to problems of relevance to therapeutic ultrasound are examined, and linear analysis is used to explain the underlying mechanisms. The dependence between the surrounding medium's elasticity (shear modulus) and the extent to which the effects of heat and mass transfer influence bubble dynamics is quantified. In particular, the oscillation properties are related to the eigenvalues determined from linear theory. Regimes under which a polytropic relation describes the heat transfer to sufficient accuracy are identified, for which the complexity and computational expense associated with solving full partial differential equations can be avoided.

FIG. 1.

(Color online) Time evolution of the bubble radius for different shear moduli for classical Rayleigh collapse using the polytropic model ($\Delta p=35p_{\infty },\hspace{0.17em}\hspace{0.17em}{R}_o=5\hspace{0.17em}\hspace{0.17em}\mu \mathrm{m}$). Ca = 0.005 (solid blue), 0.030 (dotted red), 0.600 (dashed orange), and 1000 (dashed-dotted black). Results presented in dimensionless form.

FIG. 2.

(Color online) Time evolution of the bubble radius for different shear moduli for classical Rayleigh collapse using the polytropic (dashed-dotted blue), heat transfer only (solid red), heat/mass transfer (dotted black) models ($\Delta p=35p_{\infty },\hspace{0.17em}\hspace{0.17em}{R}_o=3\hspace{0.17em}\hspace{0.17em}\mu \mathrm{m}$). Ca = 0.03 (top), 0.60 (middle), 1000 (bottom). Results presented in dimensionless form.

FIG. 3.

(Color online) Dependence of the equilibrium radius (top), time constant (middle), and damped natural frequency (bottom) on the Cauchy number for classical Rayleigh collapse based on linear analysis using the polytropic (dashed-dotted blue), heat transfer only (solid red), and heat/mass transfer (dotted black) models ($\Delta p=35p_{\infty },\hspace{0.17em}\hspace{0.17em}{R}_o=3\hspace{0.17em}\hspace{0.17em}\mu \mathrm{m}$). Results presented in dimensionless form.

FIG. 4.

(Color online) Eigenvalue map for classical Rayleigh collapse ($\Delta p=35p_{\infty },\hspace{0.17em}\hspace{0.17em}{R}_o=3\hspace{0.17em}\hspace{0.17em}\mu \mathrm{m}$), with Ca = 0.03 (black circle), 0.60 (blue square), and 1000 (green triangle). Results presented in dimensionless form.

FIG. 5.

(Color online) Temperature distribution in the surroundings for classical Rayleigh collapse ($\Delta p=35p_{\infty },\hspace{0.17em}\hspace{0.17em}{R}_o=3\hspace{0.17em}\hspace{0.17em}\mu \mathrm{m}$, Ca = 1000). Results presented in dimensionless form except for temperature (degrees Celsius).

FIG. 6.

(Color online) Time evolution of the bubble radius for different shear moduli for Flynn collapse using the polytropic model ($R_o/R_e=2.09$). Ca = 0.1 (solid blue), 1.0 (dashede-dotted red), and 10 (dotted yellow). Results presented in dimensionless form.

FIG. 7.

(Color online) Time evolution of the bubble radius for different values of shear modulus for Flynn collapse using the polytropic (dashed-dotted blue), heat transfer only (solid red), and heat/mass transfer (dotted black) models ($R_o/R_e=2.09$ for the polytropic model, $R_o/R_e=2.97$ with full thermal effects). Ca = 0.1 (top), 1.0 (middle), and 10 (bottom). Results presented in dimensionless form.

FIG. 8.

(Color online) Dependence of the time constant (top) and damped natural frequency (bottom) on the Cauchy number for Flynn collapse based on linear analysis using the polytropic (dashed-dotted blue), heat transfer only (solid red), and heat/mass transfer (dotted black) models ($R_o/R_e=2.09$ for the polytropic model, $R_o/R_e=2.97$ with full thermal effects). Results presented in dimensionless form.

FIG. 9.

(Color online) Eigenvalue map for Flynn collapse ($R_o/R_e=2.97$ with full thermal effects), with Ca = 0.1 (black circle), 1.0 (blue square), and 10 (green triangle). Results presented in dimensionless form.

FIG. 10.

(Color online) Temperature distribution in the surroundings for Flynn collapse ($R_o/R_e=2.97,\hspace{0.17em}\hspace{0.17em}\text{Ca}=0.1$). Results presented in dimensionless form, except for temperature (degrees Celsius).

FIG. 11.

(Color online) $L_{\infty }$ error in peak temperature at the bubble wall T_w (solid blue) and minimum bubble radius (dotted red) for a typical Rayleigh collapse problem as the number of points in the bubble and medium are varied. The dashed-dotted lines denote O(N) and $O(N^2)$. (Top) Interior (N_y = 1000), (Bottom) exterior (N_x = 1000).

FIG. 12.

(Color online) Time evolution of the bubble radius for the classical Rayleigh collapse problem ($\Delta p=35p_{\infty }$) with Ca = 0.03 (solid blue: full PDE model; red dotted: linearized solution). Results presented in dimensionless form.