The Bacterial Sequential Markov Coalescent

Abstract

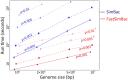
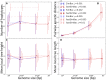
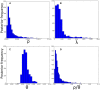
Bacteria can exchange and acquire new genetic material from other organisms directly and via the environment. This process, known as bacterial recombination, has a strong impact on the evolution of bacteria, for example, leading to the spread of antibiotic resistance across clades and species, and to the avoidance of clonal interference. Recombination hinders phylogenetic and transmission inference because it creates patterns of substitutions (homoplasies) inconsistent with the hypothesis of a single evolutionary tree. Bacterial recombination is typically modeled as statistically akin to gene conversion in eukaryotes, i.e., using the coalescent with gene conversion (CGC). However, this model can be very computationally demanding as it needs to account for the correlations of evolutionary histories of even distant loci. So, with the increasing popularity of whole genome sequencing, the need has emerged for a faster approach to model and simulate bacterial genome evolution. We present a new model that approximates the coalescent with gene conversion: the bacterial sequential Markov coalescent (BSMC). Our approach is based on a similar idea to the sequential Markov coalescent (SMC)-an approximation of the coalescent with crossover recombination. However, bacterial recombination poses hurdles to a sequential Markov approximation, as it leads to strong correlations and linkage disequilibrium across very distant sites in the genome. Our BSMC overcomes these difficulties, and shows a considerable reduction in computational demand compared to the exact CGC, and very similar patterns in simulated data. We implemented our BSMC model within new simulation software FastSimBac. In addition to the decreased computational demand compared to previous bacterial genome evolution simulators, FastSimBac provides more general options for evolutionary scenarios, allowing population structure with migration, speciation, population size changes, and recombination hotspots. FastSimBac is available from https://bitbucket.org/nicofmay/fastsimbac, and is distributed as open source under the terms of the GNU General Public License. Lastly, we use the BSMC within an Approximate Bayesian Computation (ABC) inference scheme, and suggest that parameters simulated under the exact CGC can correctly be recovered, further showcasing the accuracy of the BSMC. With this ABC we infer recombination rate, mutation rate, and recombination tract length of Bacillus cereus from a whole genome alignment.

Keywords: ABC; bacterial evolution; coalescent; recombination; simulations.

Figure 1

Graphical representation of eukaryotic and bacterial recombination models. Black circles represent sampled sequences, black lines are ancestral lineages (dashed if they represent bacterial recombination lineages). Blue segments represent the genome sequence, and red segments represent the portion of the genome that is ancestral to the particular lineage. (A) Crossover event: the entire genome to the left of the crossover site is inherited from one parent; the entire genome to the right is inherited from the other parent. (B) Gene conversion, or bacterial recombination: most of the genome is inherited from a single parent lineage, except a short segment.

Figure 2

Graphical representation of the bacterial coalescent (CGC) and BSMC models. Black circles represent sampled genomes, black lines are ancestral lineages (continuous if they belong to the clonal frame, dashed otherwise). Red segments represent, for each extant lineage, the portion of the genome that is ancestral to any sampled descendent of that lineage. Time is considered backward from bottom to top, and mergers of lineages represent coalescent events. (A) Example of simulation under the CGC; recombination and coalescent events are simulated backward in time starting with one lineage per sample at the present. (B) Example of BSMC simulation: first a clonal frame is simulated; then the process moves left to right across the genome (which for simplicity is linear), and left portions of the genome are gradually forgotten (represented in green). The BSMC stops at each recombination start and end position; recombination events are forgotten at their end, but the clonal frame is never forgotten.

Figure 3

Comparison of computational demand between the bacterial sequential Markov coalescent (BSMC) and the coalescent with gene conversion (CGC). The BSMC implemented in FastSimBac is faster than the CGC implemented in SimBac. On the vertical axis is the time required to generate local trees per replicate (in seconds on a logarithmic scale). On the horizontal axis is the genome size (in base pair on a logarithmic scale). Red lines refer to FastSimBac, blue lines to SimBac. Each point is the mean over 10 replicates, and bars represent SEs of the mean. SimBac was not run for highest recombination rates and genome sizes due to time limitations.

Figure 4

Comparison of LD and site incompatibility between the BSMC and the CGC. The BSMC generates patterns of LD (measured as $r^2$) and pairwise genetic incompatibility between sites (G4) very similar to the CGC. On the horizontal axis is the base pair distance between SNPs at which LD and G4 are measured. $r^2$ is calculated as $\left[{\left(p_{\text{AB}}-p_{\text{A}}{p}_{\text{B}}\right)}^2/p_{\text{A}}\left(1-p_{\text{A}}\right)p_{\text{B}}\left(1-p_{\text{B}}\right)\right],$ and G4 (the four-gamete test) is one if a SNP pair is incompatible and zero otherwise. For each distance d, and for any SNP x, LD and G4 are calculated between x and the first SNP at least d base pair to the right of x. Red lines refer to FastSimBac, blue lines to SimBac, and different point and line styles refer to different recombination rates (see legend). Genome length is 1 Mbp. Each point is the mean over 20 replicates, and bars are SEM. (A) Genome-wide mean LD. (B) Genome-wide mean G4.

Figure 5

Comparison of simulated patterns between the BSMC and the CGC. Bacterial evolution simulated under the BSMC generates very similar patterns to the exact CGC. (A) Genome-wide mean number of simulated haplotypes over nonoverlapping sliding windows of 10 SNPs; (B) Mean pairwise genetic distance between samples; (C) Mean local tree height; (D) Mean local tree size (sum of all branch lengths). On the horizontal axis is genome size in base pair and on logarithmic scale. Red lines refer to FastSimBac, blue lines to SimBac, and different line and dot styles indicate different recombination rates (see legend). Each point is the mean over 50 replicates, and bars are SDs. SimBac and FastSimBac were not run for the highest recombination rates and genome sizes due to time and memory limitations.

Figure 6

Accurate inference of recombination parameters with the BSMC-based ABC. Recombination parameters simulated under the exact CGC (red vertical lines) were reconstructed using simulations under the BSMC within an ABC inference scheme. Inference from another independent ABC run is shown in Figure S6 and File S1. (A) Posterior distribution of ρ. (B) Posterior distribution of λ.

Figure 7

Posterior distributions of parameters for genome-wide evolution of B. cereus. We inferred BSMC parameters using an ABC-MCMC inference scheme. (A) Posterior distribution of ρ. (B) Posterior distribution of λ. (C) Posterior distribution of θ. (D) Posterior distribution of $\rho /\theta .$