Acoustic Behavior of Halobacterium salinarum Gas Vesicles in the High-Frequency Range: Experiments and Modeling

Abstract

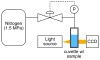
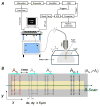
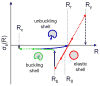
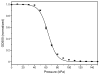
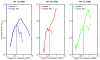
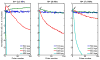
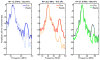
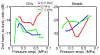
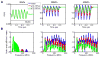
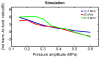
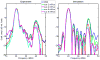
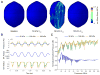
Gas vesicles (GVs) are a new and unique class of biologically derived ultrasound contrast agents with sub-micron size whose acoustic properties have not been fully elucidated. In this study, we investigated the acoustic collapse pressure and behavior of Halobacterium salinarum gas vesicles at transmit center frequencies ranging from 12.5 to 27.5 MHz. The acoustic collapse pressure was found to be above 550 kPa at all frequencies, nine-fold higher than the critical pressure observed under hydrostatic conditions. We illustrate that gas vesicles behave non-linearly when exposed to ultrasound at incident pressure ranging from 160 kPa to the collapse pressure and generate second harmonic amplitudes of -2 to -6 dB below the fundamental in media with viscosities ranging from 0.89 to 8 mPa·s. Simulations performed using a Rayleigh-Plesset-type model accounting for buckling and a dynamic finite-element analysis suggest that buckling is the mechanism behind the generation of harmonics. We found good agreement between the level of second harmonic relative to the fundamental measured at 20 MHz and the Rayleigh-Plesset model predictions. Finite-element simulations extended these findings to a non-spherical geometry, confirmed that the acoustic buckling pressure corresponds to the critical pressure under hydrostatic conditions and support the hypothesis of limited gas flow across the GV shell during the compression phase in the frequency range investigated. From simulations, estimates of GV bandwidth-limited scattering indicate that a single GV has a scattering cross section comparable to that of a red blood cell. These findings will inform the development of GV-based contrast agents and pulse sequences to optimize their detection with ultrasound.

Keywords: Buckling; Contrast agent; High-frequency ultrasound; Modeling; Submicron gas vesicles.

Figure 1

Schematic for Halo GV hydrostatic collapse pressure measurements.

Figure 2

Acoustical measurement setup (A). Schematic of the pulse transmission grid for GV collapse pressure estimation (B).

Figure 3

Shell tension as a function of effective R. In the unbuckled state and upon exposure to an acoustic pressure, shell tension varies linearly with R (red line) between the buckling radius R_b and the yield radius R_y. If during the oscillations, R reaches R_b, buckling of the shell occurs which leads to a dramatic drop of the absolute value of the shell tension (solid black arrow) followed by a slow decrease towards a plateau as R decreases (solid green line). During the unbuckling phase, shell tension further decreases to reach a value of 0 at the relaxed radius R_r, at which point the shell retrieves its unstressed state and returns to the elastic regime on expansion.

Figure 4

Halo GV optical density measurement as a function of hydrostatic pressure (N=3 independent preparations). The error bars are standard error. The data was fit to a Boltzmann sigmoid fit of the form f(p) = (1+e^{(p − p_c)/Δp} )⁻¹ with Δp = 8 kPa and an average midpoint of collapse p_c= 64 kPa (R²>0.998).

Figure 5

B-scan image of the strip of agar containing Halo GVs, after exposure to 6-cycles 20 MHz pulses at peak positive pressures ranging from 217 to 1161 kPa. Collapse of GVs is clearly visible starting at an incident pressure of 696 kPa.

Figure 6

Received power from Halo GVs in the fundamental band as a function of frequency and peak positive pressure after transmission of the 1^st and last pulses from a 100 6-cycles pulse train (PRF =1 kHz). A difference in power is clearly observed above 600 kPa, between the first and last transmitted pulse, at all frequencies, indicating collapse of part of the GV population.

Figure 7

Normalized received power from Halo GVs in the fundamental band as a function of pulse number and frequency, at peak positive pressures around collapse pressure.

Figure 8

Spectra of the signals scattered from Halo GVs and polystyrene beads, at incident pressure just below GV collapse pressure, in the frequency band of the transducers. The level of second harmonic relative to the fundamental is 10 to 15 dB higher for GVs than for beads (linear scatters), indicating GVs non linear oscillations.

Figure 9

Second harmonic-to-fundamental ratio from experiments with Halo GVs and polystyrene beads, at pressure levels below GVs collapse pressure.

Figure 10

RP simulations of GV oscillations induced by a 6-cycles 20 MHz ultrasound pulse, at 50, 300 and 600 kPa peak positive pressure: radial excursion (A), scattered pressure spectrum (B), as a function of surrounding medium viscosity (4 mPa.s corresponds to viscosity in blood).

Figure 11

Second harmonic-to-fundamental ratio obtained from RP simulation of GV oscillations in water, as function of frequency and incident peak positive pressure.

Figure 12

Spectra of backscattered signals from Halo GVs in PBS and sucrose solutions, with a 6-cycles 20-MHz ultrasound pulse, at 576 kPa: experimental results (left), RP simulation results (right). Spectra are normalized to the maximum in the fundamental frequency band.

Figure 13

FEM simulations of the deformation of a Halo GV. (A) Deformation and von Mises stress of a Halo GV filled with nitrogen gas at atmospheric pressure (100 kPa) and room temperature (300 K) for different acoustic pressures. The peak acoustic pressure and the state of the GV (i.e. maximal expansion or minimal compression volume) are indicated below each image. (B) Applied acoustic pressure (top) and the effective radius, as a function of time and peak positive pressure (middle, and bottom). (C) Fourier transforms of the radiated sound pressure due to volume changes for the different acoustic loads.

Figure 14

FEM simulations of a Halo GV with different internal gas pressures. (A) Deformation and von Mises stress for an impermeable shell containing a gas at atmospheric pressure at rest (left) or almost no gas (0.001 atm) (right), both under an acoustic load of +100 kPa. This load is just above the initial buckling pressure of 96 kPa. (B) Applied acoustic pressure (top) for a 20 MHz stimulus with an amplitude of 100 kPa and the effective radius of the GVs during simulation for the two gas contents conditions (bottom).