Correction of Selection Bias in Survey Data: Is the Statistical Cure Worse Than the Bias?

Abstract

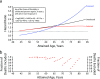
In previous articles in the American Journal of Epidemiology (Am J Epidemiol. 2013;177(5):431-442) and American Journal of Public Health (Am J Public Health. 2013;103(10):1895-1901), Masters et al. reported age-specific hazard ratios for the contrasts in mortality rates between obesity categories. They corrected the observed hazard ratios for selection bias caused by what they postulated was the nonrepresentativeness of the participants in the National Health Interview Study that increased with age, obesity, and ill health. However, it is possible that their regression approach to remove the alleged bias has not produced, and in general cannot produce, sensible hazard ratio estimates. First, we must consider how many nonparticipants there might have been in each category of obesity and of age at entry and how much higher the mortality rates would have to be in nonparticipants than in participants in these same categories. What plausible set of numerical values would convert the ("biased") decreasing-with-age hazard ratios seen in the data into the ("unbiased") increasing-with-age ratios that they computed? Can these values be encapsulated in (and can sensible values be recovered from) one additional internal variable in a regression model? Second, one must examine the age pattern of the hazard ratios that have been adjusted for selection. Without the correction, the hazard ratios are attenuated with increasing age. With it, the hazard ratios at older ages are considerably higher, but those at younger ages are well below one. Third, one must test whether the regression approach suggested by Masters et al. would correct the nonrepresentativeness that increased with age and ill health that I introduced into real and hypothetical data sets. I found that the approach did not recover the hazard ratio patterns present in the unselected data sets: the corrections overshot the target at older ages and undershot it at lower ages.

FIGURE 1—

Attempt to Recover the True Hazard Ratio Pattern After Some Data Have Been Selectively Removed Note. Panel a: In a purely mathematical population, the true hazard ratios for exposed versus not exposed participants are approximately 1.1 at the lower end of the age category and 2.5 at the upper age (black line). From this population, 19 sample waves were simulated in which, increasingly with age at potential selection, exposed persons who did participate were less likely to die in the next six years than were their sampled unexposed peers who did not participate. This attenuated the observed hazard ratio curve (red line). Panel b: The selectivity that increases with age excludes some of the exposed persons who are so ill that they will die within six years. For example, the six red dots beginning at age 65 years (a potential age at entry) indicate what fractions of these frail 65-year-old individuals who die in the next six years were excluded from the survey wave. Applied to these selective data, the approach proposed by Masters et al. (panel a, blue line) was not able to recover the hazard pattern present in the unselected data.