Detecting and characterizing high-frequency oscillations in epilepsy: a case study of big data analysis
- PMID: 28280577
- PMCID: PMC5319343
- DOI: 10.1098/rsos.160741
Detecting and characterizing high-frequency oscillations in epilepsy: a case study of big data analysis
Abstract
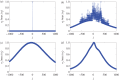
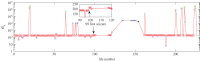
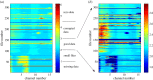
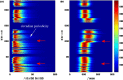
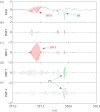
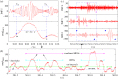
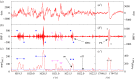
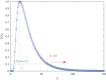
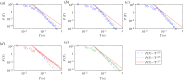
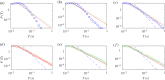
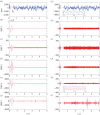
We develop a framework to uncover and analyse dynamical anomalies from massive, nonlinear and non-stationary time series data. The framework consists of three steps: preprocessing of massive datasets to eliminate erroneous data segments, application of the empirical mode decomposition and Hilbert transform paradigm to obtain the fundamental components embedded in the time series at distinct time scales, and statistical/scaling analysis of the components. As a case study, we apply our framework to detecting and characterizing high-frequency oscillations (HFOs) from a big database of rat electroencephalogram recordings. We find a striking phenomenon: HFOs exhibit on-off intermittency that can be quantified by algebraic scaling laws. Our framework can be generalized to big data-related problems in other fields such as large-scale sensor data and seismic data analysis.
Keywords: big data analysis; electroencephalogram; empirical modedecomposition; epileptic seizures; high-frequency oscillations; nonlinear dynamics.
Figures
References
-
- Marx V. 2013. Biology: the big challenges of big data. Nature (London) 498, 255–260. (doi:10.1038/498255a) - DOI - PubMed
-
- Sagiroglu S, Sinanc D. 2013. Big data: a review. In 2013 Int. Conf. on Collaboration Technologies and Systems (CTS), San Diego, CA, pp. 42–47. IEEE.
-
- Katal A, Wazid M, Goudar RH. 2013. Big data: issues, challenges, tools and good practices. In Sixth Int. Conf. on Contemporary Computing (IC3), Noida, pp. 404–409. IEEE.
-
- Chen M, Mao SW, Zhang Y, Leung VCM. 2014. Big data related technologies, challenges and future prospects. Berlin, Germany: Springer.
-
- Fan JQ, Han F, Liu H. 2014. Challenges of big data analysis. Nat. Sci. Rev. 1, 293–314. (doi:10.1093/nsr/nwt032) - DOI - PMC - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
