Disease dynamics in a stochastic network game: a little empathy goes a long way in averting outbreaks

Abstract

Individuals change their behavior during an epidemic in response to whether they and/or those they interact with are healthy or sick. Healthy individuals may utilize protective measures to avoid contracting a disease. Sick individuals may utilize preemptive measures to avoid spreading a disease. Yet, in practice both protective and preemptive changes in behavior come with costs. This paper proposes a stochastic network disease game model that captures the self-interests of individuals during the spread of a susceptible-infected-susceptible disease. In this model, individuals strategically modify their behavior based on current disease conditions. These reactions influence disease spread. We show that there is a critical level of concern, i.e., empathy, by the sick individuals above which disease is eradicated rapidly. Furthermore, we find that risk averse behavior by the healthy individuals cannot eradicate the disease without the preemptive measures of the sick individuals. Empathy is more effective than risk-aversion because when infectious individuals change behavior, they reduce all of their potential infections, whereas when healthy individuals change behavior, they reduce only a small portion of potential infections. This imbalance in the role played by the response of the infected versus the susceptible individuals on disease eradication affords critical policy insights.

Figure 1. SIS Markov chain dynamics.

We show one step of the Markov chain dynamics in (a) where circles denote individuals who are healthy (open) or sick (shaded). The edges denote contacts, where the actions are indicated by the edge-end types, social distancing | and interaction . Given the state of the disease and contact network at time t, individuals decide to take preemptive measures or not at time t+ which determines the state of each individual at time t + 1 according to the Markov chain dynamics in (7). If a_i = 1, individual i does not take any preemptive measures. If a_i = 0, i self-isolates reducing any risk of disease contraction or spread to zero. A healthy individual can only contract the disease from an interaction with a neighbor if and only if the individual’s neighbor is infected and neither of the two self-isolates. These interactions are marked by a red dot in the middle figure. We enumerate each pair of state and action in (b).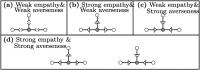

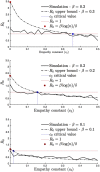
Figure 2. MMPE equilibrium strategy actions with respect to utility constants.

There are n = 4 individuals forming a star network. In cases (a–c) the stage equilibrium action is unique. In case (d) there two stage equilibria. When risk averseness is weak, i.e., c₀ > c₁, all healthy individuals take action a_i = 1 regardless of the action of the center individual. When empathy is weak, i.e., c₀ > 3c₂, the sick individual at the center takes action a_i = 1 regardless of i’s neighbors’ actions by the same reasoning. Based on these responses we can solve for stage equilibrium in (a–c). In (a) (c₀ > c₁ and c₀ > 3c₂), all individuals take action 1. In (b), because all healthy individuals take action 1 due to weak averseness, the sick individual takes action 0 considering the strong empathy (c₀ < 3c₂). In (c), because the sick individual takes action 1 due to weak empathy, all healthy individuals take action 0 considering their strong averseness (c₀ < c₁). In (d), if healthy individuals take action 1 then it is in the interest of the strongly empathetic sick individual to take action 0. However, if healthy individuals take action 0 then the sick individual receives a positive payoff from taking action 1. In both cases no individual has an incentive to deviate to another action.

Figure 3. Behavior and disease dynamics with respect to payoff constants.

The red and black lines in the figures correspond to payoff constants with weak and strong empathy, respectively. In both setups we have β = 0.4, δ = 0.2, c₀ = 1 and weak averseness (c₀ > c₁). In particular, we consider risk aversion constant c₁ to be 3c₁ > c₀ > 2c₁. The MMPE action for the strong empathy case is given by Fig. 2(b). The MMPE action at time t = 1 for weak empathy is given by Fig. 2(a). The sequence of networks at the top shows the disease state and MMPE action of each individual at each time on the network for the weak empathy & weak averseness case. In this case, the MMPE actions are such that all individuals socialize at all times unless a healthy individual has three sick neighbors when the healthy individual self-isolates–see times 12 and 13. This is because of the value of the risk aversion constant obeys the relation 3c₁ > c₀. Bottom figure represents the corresponding aggregate utility for each case.

Figure 4. Accuracy of the critical empathy c₂ threshold for R₀ < 1.

We consider n = 100 individuals and set the constants as δ = 0.2, c₀ = 1 and c₁ = 0.24. We let for top, middle, and bottom figures, respectively. The dotted dashed lines are the R₀ upper bound value (2) with respect to the c₂ value on x-axis. For c₂ = 0, we have the red circled points corresponding to the R₀ upper bound when there is no behavior response by the initial sick individual. Note that all the red circled points indicate R₀ > 1. From (3), the critical values of c₂ that make R₀ < 1 equal to 0.02, 0.16, and 0.36 for , respectively. These points are marked in blue. R₀ upper bound increases linear in β according to (2). We simulate R₀ values as follows. We generate a scale-free network with γ = 2 according to the preferential attachment algorithm. For each β and c₂ value pair, we consider 100 realizations with randomly selecting patient zero and counting the number of individuals infected by patient zero until patient zero heals. Each point in the solid lines corresponds to the average of the total count values in 100 initializations. We observe that the simulated average R₀ is less than one above the critical c₂ value in (3).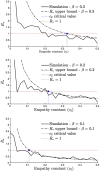

Figure 5. Accuracy of the critical empathy c₂ threshold for .

We consider n = 100 individuals and set the constants as δ = 0.2, c₀ = 1 and c₁ = 0.24. We let for top, middle, and bottom figures, respectively. The dotted dashed lines are the bound value in (5) with respect to the c₂ value on the x-axis. The critical values of c₂ in (6) that make are 0.11, 0.22 and 0.33 respectively for . These points are marked in blue. We simulate values identical to the way we simulate R₀ values in Fig. 4 except that we select the initial sick individual according to distribution Q(k). We observe the simulated values are less than one for all c₂ values above the critical value in (6). In comparison the critical c₂ values for R₀ in (3)–see Fig. 4–do not accurately predict the values of c₂ above which .

Figure 6. Effect of risk averseness c₁ and empathy c₂ constants on eradication.

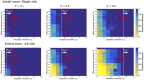
We consider n = 100 individuals, and let δ = 0.2, and c₀ = 1. The infection rate β values equal to 0.1, 0.2 and 0.3 for figures left, middle, and right, respectively. The runs start with a single infected individual and all individuals infected respectively for the top and bottom figures. In each plot, the axes correspond to the constant values of c₁ and c₂. For a given value of c₁ and c₂, we generate 50 scale-free networks using the preferential attachment algorithm and run the stochastic network disease game for 200 steps for each network. The grid color represents the ratio of runs in which disease is eradicated within 200 steps. For figures left, middle, and right the eradication of threshold is equal to 2.65, 5.3, and 8, respectively. That is, for all the figures. The critical values of the empathy constant, that make R₀ < 1 for calculated using (6) are marked with white dotted dashed lines. The critical values of the empathy constant, , that make for calculated using (6) are accurate in determining fast eradication for any value of c₁ (marked with red solid lines).