Review of interferometric spectroscopy of scattered light for the quantification of subdiffractional structure of biomaterials
- PMID: 28290596
- PMCID: PMC5348632
- DOI: 10.1117/1.JBO.22.3.030901
Review of interferometric spectroscopy of scattered light for the quantification of subdiffractional structure of biomaterials
Abstract
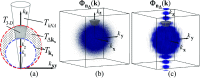
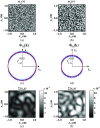
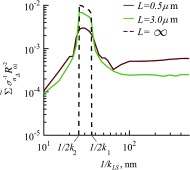
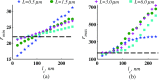
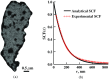
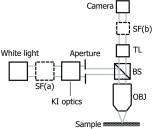
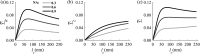
Optical microscopy is the staple technique in the examination of microscale material structure in basic science and applied research. Of particular importance to biology and medical research is the visualization and analysis of the weakly scattering biological cells and tissues. However, the resolution of optical microscopy is limited to ? 200 ?? nm due to the fundamental diffraction limit of light. We review one distinct form of the spectroscopic microscopy (SM) method, which is founded in the analysis of the second-order spectral statistic of a wavelength-dependent bright-field far-zone reflected-light microscope image. This technique offers clear advantages for biomedical research by alleviating two notorious challenges of the optical evaluation of biomaterials: the diffraction limit of light and the lack of sensitivity to biological, optically transparent structures. Addressing the first issue, it has been shown that the spectroscopic content of a bright-field microscope image quantifies structural composition of samples at arbitrarily small length scales, limited by the signal-to-noise ratio of the detector, without necessarily resolving them. Addressing the second issue, SM utilizes a reference arm, sample arm interference scheme, which allows us to elevate the weak scattering signal from biomaterials above the instrument noise floor.
Figures
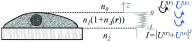






Similar articles
-
Interferometric spectroscopy of scattered light can quantify the statistics of subdiffractional refractive-index fluctuations.Phys Rev Lett. 2013 Jul 19;111(3):033903. doi: 10.1103/PhysRevLett.111.033903. Epub 2013 Jul 19. Phys Rev Lett. 2013. PMID: 23909326 Free PMC article.
-
What structural length scales can be detected by the spectral variance of a microscope image?Opt Lett. 2014 Aug 1;39(15):4290-3. doi: 10.1364/OL.39.004290. Opt Lett. 2014. PMID: 25078159 Free PMC article.
-
Reconstruction of explicit structural properties at the nanoscale via spectroscopic microscopy.J Biomed Opt. 2016 Feb;21(2):25007. doi: 10.1117/1.JBO.21.2.025007. J Biomed Opt. 2016. PMID: 26886803 Free PMC article.
-
Phase recovery and lensless imaging by iterative methods in optical, X-ray and electron diffraction.Philos Trans A Math Phys Eng Sci. 2002 May 15;360(1794):875-95. doi: 10.1098/rsta.2001.0972. Philos Trans A Math Phys Eng Sci. 2002. PMID: 12804284 Review.
-
Anatomy of noise in quantitative biological Raman spectroscopy.Bioanalysis. 2014 Feb;6(3):411-21. doi: 10.4155/bio.13.337. Bioanalysis. 2014. PMID: 24471960 Review.
Cited by
-
Label-Free and Quantitative Dry Mass Monitoring for Single Cells during In Situ Culture.Cells. 2021 Jun 29;10(7):1635. doi: 10.3390/cells10071635. Cells. 2021. PMID: 34209893 Free PMC article.
-
Label-free tomography of living cellular nanoarchitecture using hyperspectral self-interference microscopy.Biomed Opt Express. 2019 May 13;10(6):2757-2767. doi: 10.1364/BOE.10.002757. eCollection 2019 Jun 1. Biomed Opt Express. 2019. PMID: 31259049 Free PMC article.
-
Multimodal interference-based imaging of nanoscale structure and macromolecular motion uncovers UV induced cellular paroxysm.Nat Commun. 2019 Apr 10;10(1):1652. doi: 10.1038/s41467-019-09717-6. Nat Commun. 2019. PMID: 30971691 Free PMC article.
-
Probing Field Cancerization in the Gastrointestinal Tract Using a Hybrid Raman and Partial Wave Spectroscopy Microscope.Anal Chem. 2025 Jun 24;97(24):12642-12653. doi: 10.1021/acs.analchem.5c00954. Epub 2025 Jun 11. Anal Chem. 2025. PMID: 40497475 Free PMC article.
-
Nanoscale chromatin imaging and analysis platform bridges 4D chromatin organization with molecular function.Sci Adv. 2021 Jan 1;7(1):eabe4310. doi: 10.1126/sciadv.abe4310. Print 2021 Jan. Sci Adv. 2021. PMID: 33523864 Free PMC article.
References
-
- Alexandrov S., Sampson D., “Spatial information transmission beyond a system’s diffraction limit using optical spectral encoding of the spatial frequency,” J. Opt. A: Pure Appl. Opt. 10(2), 025304 (2008).10.1088/1464-4258/10/2/025304 - DOI
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

