Memory effects on epidemic evolution: The susceptible-infected-recovered epidemic model

Abstract

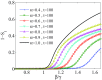
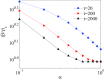
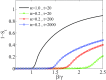
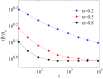
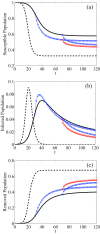
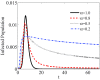
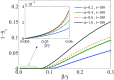
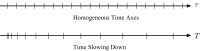
Memory has a great impact on the evolution of every process related to human societies. Among them, the evolution of an epidemic is directly related to the individuals' experiences. Indeed, any real epidemic process is clearly sustained by a non-Markovian dynamics: memory effects play an essential role in the spreading of diseases. Including memory effects in the susceptible-infected-recovered (SIR) epidemic model seems very appropriate for such an investigation. Thus, the memory prone SIR model dynamics is investigated using fractional derivatives. The decay of long-range memory, taken as a power-law function, is directly controlled by the order of the fractional derivatives in the corresponding nonlinear fractional differential evolution equations. Here we assume "fully mixed" approximation and show that the epidemic threshold is shifted to higher values than those for the memoryless system, depending on this memory "length" decay exponent. We also consider the SIR model on structured networks and study the effect of topology on threshold points in a non-Markovian dynamics. Furthermore, the lack of access to the precise information about the initial conditions or the past events plays a very relevant role in the correct estimation or prediction of the epidemic evolution. Such a "constraint" is analyzed and discussed.

FIG. 1.

Outbreak size $1-S_t$ for a SIR system having evolved until time $t=100$, vs the parameter defining the threshold: $\beta /\gamma$, when including memory effects. Each curve corresponds to a different value of $\alpha$, as indicated in the inset. As $\alpha$ decreases, the epidemic threshold ${(\beta /\gamma )}_c$ shifts to higher values.

FIG. 2.

Variation of threshold point vs $\alpha$ for different finite times $t=20,200,2000$. For each time, the epidemic threshold is shifted to higher values with decreasing $\alpha$. The axes are logarithmic and the numbers are presented as base 10 exponential notation.

FIG. 3.

Order parameter $1-S_t$ for a SIR system having evolved until time $t$, when including much memory ($\alpha =0.2$). Each curve corresponds to a different finite time $t$, as indicated in the inset. The threshold values can be compared with that of the corresponding epidemic threshold for a memoryless system, i.e., when $\alpha =1$ (and $t=20$). The curves for $\alpha =1$ at $t=200$ and $t=2000$ are not drawn for better readability.

FIG. 4.

Variation of threshold point vs $t$ for different values of $\alpha =0.2,0.5,0.8$. For each $\alpha$, the epidemic threshold is shifted to lower values with increasing finite time. The axes are logarithmic and the numbers are presented as base 10 exponential notation.

FIG. 5.

Effect of different initial times on the dynamics of a non-Markovian process. The curves denote the fraction of (a) susceptible, (b) infected, and (c) removed individuals. Dashed and solid lines correspond to Markovian and non-Markovian processes, respectively, started from $t=0$. The curves with symbols correspond to the dynamics of non-Markovian processes, started from nonzero initial times with different initial conditions.

FIG. 6.

Fraction of infected individuals versus time for the SIR model on a scale-free network with degree exponent $\lambda =3$ and for different values of $\alpha$.

FIG. 7.

Outbreak size, $1-S_t$, for the SIR model on a scale-free network with degree exponent $\lambda =3$ in terms of $\beta /\gamma$. The dynamics is evolved until time $t=100$, when including memory effects. Each curve corresponds to a different value of $\alpha$, as indicated in the insert.

FIG. 8.

Schematic comparison between homogeneous and fractional time axes.