Observation of anomalous Hall effect in a non-magnetic two-dimensional electron system

Abstract

Anomalous Hall effect, a manifestation of Hall effect occurring in systems without time-reversal symmetry, has been mostly observed in ferromagnetically ordered materials. However, its realization in high-mobility two-dimensional electron system remains elusive, as the incorporation of magnetic moments deteriorates the device performance compared to non-doped structure. Here we observe systematic emergence of anomalous Hall effect in various MgZnO/ZnO heterostructures that exhibit quantum Hall effect. At low temperatures, our nominally non-magnetic heterostructures display an anomalous Hall effect response similar to that of a clean ferromagnetic metal, while keeping a large anomalous Hall effect angle θ_AHE≈20°. Such a behaviour is consistent with Giovannini-Kondo model in which the anomalous Hall effect arises from the skew scattering of electrons by localized paramagnetic centres. Our study unveils a new aspect of many-body interactions in two-dimensional electron systems and shows how the anomalous Hall effect can emerge in a non-magnetic system.

Figure 1. Concept of anomalous Hall effect.

(a) Hall voltage is built in the magnetic field B due to the Lorentz force (left panel) and due to the spin–orbit coupling in ferromagnetic material with the total magnetization M (right panel). (b) Appearance of anomalous Hall effect: electrons are deflected in the mean field of spontaneously ordered magnetic moments. (c) Anomalous Hall effect in a paramagnetic system, such as ZnO, is brought about by the spin-dependent electron scattering on localized magnetic moment J. (d) Schematic representation of anomalous Hall effect scaling behaviour found in various materials.

Figure 2. Sample characteristics establish the anomalous Hall effect.

(a) Magnetotransport R_xx and R_yx at two representative temperatures. (b) Anomalous Hall effect component at different temperatures. The Landau level integer filling factors ν becomes visible at T<8 K. (c) Temperature dependence of the charge carrier density extracted from the ordinary Hall effect in high field. (d) Four-point resistance R_xx as a function of temperature. (e) Temperature dependence of the saturated value of anomalous Hall effect resistance . 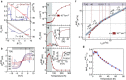(f) AHE scaling: ∝. α=0.94±0.08 is observed between 2 and 10 K, whereas α>1 at higher temperature. (g) AHE angle increases with the decreasing temperature.

Figure 3. Magnetic characteristics deduced from electrical transport.

(a) Temperature dependence of the anomalous Hall effect normalized to the saturated value of AHE. Such a representation makes apparent the similarity with the magnetization behaviour of a paramagnetic system. The Brillouin function describes well the field dependence of AHE. (b) Left axis: temperature dependence of μ_B obtained from the fitting the AHE traces in a with the Brillouin function. Right axis: temperature dependence of the slope of AHE around B=0 in a. (c) Magnetic susceptibility χ obtained from the slope of AHE and temperature dependence μ_B. For T<10 K, the dependence of 1/χ on T can be approximated with the Curie–Weiss law (black line).

Figure 4. Anomalous Hall effect scaling.

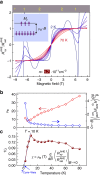
(a) Scaling of anomalous Hall effect ∝ with α=1 (blue solid line) at low temperature is observed for structures covering a wide range of charge carrier density. For clarity of representation, for each sample is multiplied by a factor shown in the box. α increases at elevated temperature. (b) The inverse spin-susceptibility 1/χ peaks at some temperature indicated by solid symbol (except the highest density sample) and suggests the change in the system's magnetic property. This transition temperature is higher for higher carrier density samples and correlates with the temperature at which α starts deviating from 1, except the samples E–G with the higher carrier concentration. At low temperature, 1/χ versus T dependence can be approximated with the Curie–Weiss law with a characteristic temperature T_cw. (c) Temperature dependence of AHE angle for all samples. The AHE angle lies in the range between tan(θ_AHE)=0.3 and tan(θ_AHE)=0.5 at T=2 K, indicating a non-vanishing AHE at low temperature. (d) T_cw increases with the increasing carrier density. Error bar is given by the uncertainty with which the linear dependence 1/χ versus T can be approximated in b.