Is the Bethe-Salpeter Formalism Accurate for Excitation Energies? Comparisons with TD-DFT, CASPT2, and EOM-CCSD

Abstract

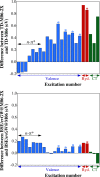
Developing ab initio approaches able to provide accurate excited-state energies at a reasonable computational cost is one of the biggest challenges in theoretical chemistry. In that framework, the Bethe-Salpeter equation approach, combined with the GW exchange-correlation self-energy, which maintains the same scaling with system size as TD-DFT, has recently been the focus of a rapidly increasing number of applications in molecular chemistry. Using a recently proposed set encompassing excitation energies of many kinds [J. Phys. Chem. Lett. 2016, 7, 586-591], we investigate here the performances of BSE/GW. We compare these results to CASPT2, EOM-CCSD, and TD-DFT data and show that BSE/GW provides an accuracy comparable to the two wave function methods. It is particularly remarkable that the BSE/GW is equally efficient for valence, Rydberg, and charge-transfer excitations. In contrast, it provides a poor description of triplet excited states, for which EOM-CCSD and CASPT2 clearly outperform BSE/GW. This contribution therefore supports the use of the Bethe-Salpeter approach for spin-conserving transitions.

Figure 1

Variation of the excitation energies when changing the functional from M06 to M06-2X at the TD-DFT (top) and BSE/evGW (bottom) levels. The states are ordered as in Table 1. The blue, red, and green histograms correspond to valence, Rydberg, and CT transitions, respectively. The stars indicate the singlet–triplet transitions.