Experimental comparison of two quantum computing architectures

Abstract

We run a selection of algorithms on two state-of-the-art 5-qubit quantum computers that are based on different technology platforms. One is a publicly accessible superconducting transmon device (www.

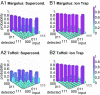
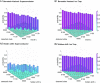
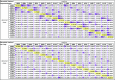
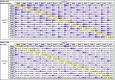
Research: ibm.com/ibm-q) with limited connectivity, and the other is a fully connected trapped-ion system. Even though the two systems have different native quantum interactions, both can be programed in a way that is blind to the underlying hardware, thus allowing a comparison of identical quantum algorithms between different physical systems. We show that quantum algorithms and circuits that use more connectivity clearly benefit from a better-connected system of qubits. Although the quantum systems here are not yet large enough to eclipse classical computers, this experiment exposes critical factors of scaling quantum computers, such as qubit connectivity and gate expressivity. In addition, the results suggest that codesigning particular quantum applications with the hardware itself will be paramount in successfully using quantum computers in the future.

Keywords: quantum computing; quantum computing architecture; quantum information; quantum information science; quantum physics.

Fig. 1.

Graphic representations of the two systems. (A) the superconducting qubits connected by microwave resonators (credit: IBM Research). (B) The linear chain of trapped ions connected by laser-mediated interactions. (A and B, Insets) Qubit connectivity graphs: (A) star shaped and (B) fully connected.

Fig. 2.

High-level circuits of the implemented example computations (gates defined in ref. 15). (A–D) Margolus gate (A), Toffoli gate (B), Bernstein–Vazirani (C), and hidden shift (D). The Bernstein–Vazirani algorithm is shown for the oracle $c=(1111)$, where all CNOTs are present. The hidden shift circuit is shown for the shift pattern $s=(1011)$, where X operations are present on qubits $1$, $3$, and $4$.

Fig. 3.

Margolus gate results from the star-shaped superconductor (A1) and the fully connected ion trap system (B1). The fidelities are $74.1(7)$% and $90.1(2)\%$, respectively. The full Toffoli gate results give success probabilities of $52.6(8)\%$ for the superconducting (A2) and $85.0(2)\%$ for the ion-trap (B2) system. The axes represent states as $3$-bit binary numbers. For each input state, the probabilities of detecting each state are shown.

Fig. 4.

Results from the Bernstein–Vazirani algorithm implementing the oracle function $f_c(x)=x_0{c}_0\oplus c_1{x}_1\oplus c_2{x}_2\oplus c_3{x}_3$ for all possible $4$-bit oracles c performed on the star-shaped (A1) and the fully connected (B1) systems. The average success probabilities are $72.8(5)\%$ for the superconductor and $85.1(1)\%$ for the ion-trap system. The hidden shift algorithm for $f(x)=x_0{x}_1\oplus x_2{x}_3$. All possible $4$-bit shifted oracle functions are implemented on the superconducting system (A2) as well as the ion trap (B2). The average success probabilities are $35.1(6)$% and $77.1(2)\%$, respectively. The axes represent states and oracle parameters as $4$-bit binary numbers.

Fig. S1.

Numerical quantum computer 3-qubit input/output matrix for the Margolus gate (Top two panels) and the Toffoli gate (Bottom two panels), corresponding to Fig. 3 of the main text. For each gate, the results from both superconductor and ion-trap quantum computers are displayed.

Fig. S2.

Numerical quantum computer 4-qubit input/output matrix for the Berstein–Vazirani algorithm for the superconductor system (Top) and the ion-trap system (Bottom), corresponding to Fig. 4 A1 and B1 of the main text.

Fig. S3.

Numerical quantum computer 4-qubit input/output matrix for the hidden shift algorithm for the superconductor system (Top) and the ion-trap system (Bottom), corresponding to Fig. 4 A2 and B2 of the main text.