Decreased integration and information capacity in stroke measured by whole brain models of resting state activity
- PMID: 28334882
- PMCID: PMC6075429
- DOI: 10.1093/brain/awx021
Decreased integration and information capacity in stroke measured by whole brain models of resting state activity
Abstract
While several studies have shown that focal lesions affect the communication between structurally normal regions of the brain, and that these changes may correlate with behavioural deficits, their impact on brain's information processing capacity is currently unknown. Here we test the hypothesis that focal lesions decrease the brain's information processing capacity, of which changes in functional connectivity may be a measurable correlate. To measure processing capacity, we turned to whole brain computational modelling to estimate the integration and segregation of information in brain networks. First, we measured functional connectivity between different brain areas with resting state functional magnetic resonance imaging in healthy subjects (n = 26), and subjects who had suffered a cortical stroke (n = 36). We then used a whole-brain network model that coupled average excitatory activities of local regions via anatomical connectivity. Model parameters were optimized in each healthy or stroke participant to maximize correlation between model and empirical functional connectivity, so that the model's effective connectivity was a veridical representation of healthy or lesioned brain networks. Subsequently, we calculated two model-based measures: 'integration', a graph theoretical measure obtained from functional connectivity, which measures the connectedness of brain networks, and 'information capacity', an information theoretical measure that cannot be obtained empirically, representative of the segregative ability of brain networks to encode distinct stimuli. We found that both measures were decreased in stroke patients, as compared to healthy controls, particularly at the level of resting-state networks. Furthermore, we found that these measures, especially information capacity, correlate with measures of behavioural impairment and the segregation of resting-state networks empirically measured. This study shows that focal lesions affect the brain's ability to represent stimuli and task states, and that information capacity measured through whole brain models is a theory-driven measure of processing capacity that could be used as a biomarker of injury for outcome prediction or target for rehabilitation intervention.
Keywords: functional connectivity; information capacity; integration; whole-brain modelling.
© The Author (2017). Published by Oxford University Press on behalf of the Guarantors of Brain. All rights reserved. For Permissions, please email: journals.permissions@oup.com.
Figures


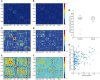
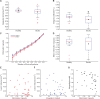


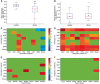
Comment in
-
Defining a functional network homeostasis after stroke: EEG-based approach is complementary to functional MRI.Brain. 2017 Dec 1;140(12):e71. doi: 10.1093/brain/awx271. Brain. 2017. PMID: 29112697 No abstract available.
-
Reply: Defining a functional network homeostasis after stroke: EEG-based approach is complementary to functional MRI.Brain. 2017 Dec 1;140(12):e72. doi: 10.1093/brain/awx277. Brain. 2017. PMID: 29112703 Free PMC article. No abstract available.
References
-
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc Ser B Methodol 1995; 57: 289–300.
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

