Basis-neutral Hilbert-space analyzers
- PMID: 28344331
- PMCID: PMC5366812
- DOI: 10.1038/srep44995
Basis-neutral Hilbert-space analyzers
Abstract
Interferometry is one of the central organizing principles of optics. Key to interferometry is the concept of optical delay, which facilitates spectral analysis in terms of time-harmonics. In contrast, when analyzing a beam in a Hilbert space spanned by spatial modes - a critical task for spatial-mode multiplexing and quantum communication - basis-specific principles are invoked that are altogether distinct from that of 'delay'. Here, we extend the traditional concept of temporal delay to the spatial domain, thereby enabling the analysis of a beam in an arbitrary spatial-mode basis - exemplified using Hermite-Gaussian and radial Laguerre-Gaussian modes. Such generalized delays correspond to optical implementations of fractional transforms; for example, the fractional Hankel transform is the generalized delay associated with the space of Laguerre-Gaussian modes, and an interferometer incorporating such a 'delay' obtains modal weights in the associated Hilbert space. By implementing an inherently stable, reconfigurable spatial-light-modulator-based polarization-interferometer, we have constructed a 'Hilbert-space analyzer' capable of projecting optical beams onto any modal basis.
Conflict of interest statement
The authors declare no competing financial interests.
Figures
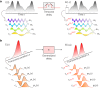
 (angular frequencies ω) each with a spectral amplitude cn. The delayed pulse E(t − τ) is the result of inserting phase factors
(angular frequencies ω) each with a spectral amplitude cn. The delayed pulse E(t − τ) is the result of inserting phase factors  for each harmonic ω. (b) Generalized delay (GD) α in a Hilbert space spanned by a discrete modal basis
for each harmonic ω. (b) Generalized delay (GD) α in a Hilbert space spanned by a discrete modal basis  . The impact of the GD on an optical beam can also be viewed in two domains. In the spatial domain (first row), the GD is not simply a shift but instead it transforms the transverse field profile E(x) → E(x; α). However, in the modal space (second row) where the field is viewed as a superposition of the modes
. The impact of the GD on an optical beam can also be viewed in two domains. In the spatial domain (first row), the GD is not simply a shift but instead it transforms the transverse field profile E(x) → E(x; α). However, in the modal space (second row) where the field is viewed as a superposition of the modes  with weights
with weights  , the impact of the GD is identical to that of the temporal delay on the spectral harmonics in (a). The GD adds a phase factor
, the impact of the GD is identical to that of the temporal delay on the spectral harmonics in (a). The GD adds a phase factor  to the
to the  mode amplitude, which ‘delays’ the beam by α in the Hilbert space spanned by
mode amplitude, which ‘delays’ the beam by α in the Hilbert space spanned by  .
.
 – is collected by a bucket detector and an interferogram is recorded with α,
– is collected by a bucket detector and an interferogram is recorded with α,  , whose Fourier transform reveals the modal weights
, whose Fourier transform reveals the modal weights  . (b) Operation of the generalized interferometer in the Hilbert space spanned by the modal basis
. (b) Operation of the generalized interferometer in the Hilbert space spanned by the modal basis  on the beam
on the beam  (Fig. 1b). The underlying modes of the ‘delayed’ copy acquire phase shifts of the form
(Fig. 1b). The underlying modes of the ‘delayed’ copy acquire phase shifts of the form  after passing through the GD to yield a new beam
after passing through the GD to yield a new beam  . The original and ‘delayed’ beams are combined
. The original and ‘delayed’ beams are combined  to produce an interferogram
to produce an interferogram  . Because the modes are orthogonal to each other, each interferes only with its phase-shifted counterpart to yield an interferogram of the form 1 + cos nα with weights
. Because the modes are orthogonal to each other, each interferes only with its phase-shifted counterpart to yield an interferogram of the form 1 + cos nα with weights  – independently of the underlying basis
– independently of the underlying basis  that is traced out at the bucket detector. The sought-after weights are then revealed through harmonic analysis.
that is traced out at the bucket detector. The sought-after weights are then revealed through harmonic analysis.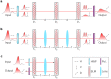
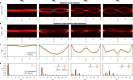
 . Each vertical line plot represents the magnitude-squared of a 1D fFT
. Each vertical line plot represents the magnitude-squared of a 1D fFT  associated with a different order α. (b) The measured interferogram resulting from superposing the delayed beam from (a) with a reference,
associated with a different order α. (b) The measured interferogram resulting from superposing the delayed beam from (a) with a reference,  . Each vertical line plot thus represents the magnitude-squared of the 1D spatial interferogram associated with a different order α. (c) The integrated interferogram
. Each vertical line plot thus represents the magnitude-squared of the 1D spatial interferogram associated with a different order α. (c) The integrated interferogram  . This interferogram is now basis-neutral. (d) The modal weights |cn|2 revealed by taking the Fourier transform of the interferogram in (c). The columns are for different input beams corresponding to modes HG0 through HG3. The implemented beams only approximate the pure HG modes (except for HG0 which is exact), as shown in the insets in (d). The black mode profile in the inset is an exact HG mode while the orange plot is the approximate beam used in the experiment. The theory plots in (c) and (d) are those for the implemented approximate beams. See Supplementary Information for theory.
. This interferogram is now basis-neutral. (d) The modal weights |cn|2 revealed by taking the Fourier transform of the interferogram in (c). The columns are for different input beams corresponding to modes HG0 through HG3. The implemented beams only approximate the pure HG modes (except for HG0 which is exact), as shown in the insets in (d). The black mode profile in the inset is an exact HG mode while the orange plot is the approximate beam used in the experiment. The theory plots in (c) and (d) are those for the implemented approximate beams. See Supplementary Information for theory.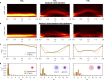
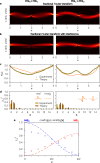
 (left column) and
(left column) and  (right column). (e) Modal analysis of the beam
(right column). (e) Modal analysis of the beam  , while varying θ from 0 to π/2. Plotted are the coefficients |c0|2 (blue squares) and |c1|2 (red circles), corresponding to the contributions of the modes HG0 and HG1. Dashed curves are theoretical predictions, for |c0|2 and |c1|2 predicated on the generated approximate modes.
, while varying θ from 0 to π/2. Plotted are the coefficients |c0|2 (blue squares) and |c1|2 (red circles), corresponding to the contributions of the modes HG0 and HG1. Dashed curves are theoretical predictions, for |c0|2 and |c1|2 predicated on the generated approximate modes.References
-
- Kipnis N.. History of the Principle of Interference of Light(Birkhäuser Verlag, 1991).
-
- Young T.. “Experimental demonstration of the general law of the interference of light”, Phil. Trans. Royal Soc. London 94, 1–16 (1804).
-
- Hanbury Brown R. & Twiss R. Q.. “Correlation between photons in two coherent beams of light”, Nature 177, 27–29 (1956).
-
- Taylor G. I.. “Interference fringes with feeble light”, Proc. Cam. Phil. Soc. 15, 114–115 (1909).
-
- Grangier P., Roger G. & Aspect A.. “Experimental evidence for a photon anticorrelation effect on a beam splitter: A new light on single-photon interferences”, Europhys. Lett. 1, 173–179 (1986).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

