Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight
- PMID: 28355184
- PMCID: PMC5412966
- DOI: 10.1038/nature21727
Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight
Abstract
Mosquitoes exhibit unusual wing kinematics; their long, slender wings flap at remarkably high frequencies for their size (>800 Hz)and with lower stroke amplitudes than any other insect group. This shifts weight support away from the translation-dominated, aerodynamic mechanisms used by most insects, as well as by helicopters and aeroplanes, towards poorly understood rotational mechanisms that occur when pitching at the end of each half-stroke. Here we report free-flight mosquito wing kinematics, solve the full Navier-Stokes equations using computational fluid dynamics with overset grids, and validate our results with in vivo flow measurements. We show that, although mosquitoes use familiar separated flow patterns, much of the aerodynamic force that supports their weight is generated in a manner unlike any previously described for a flying animal. There are three key features: leading-edge vortices (a well-known mechanism that appears to be almost ubiquitous in insect flight), trailing-edge vortices caused by a form of wake capture at stroke reversal, and rotational drag. The two new elements are largely independent of the wing velocity, instead relying on rapid changes in the pitch angle (wing rotation) at the end of each half-stroke, and they are therefore relatively immune to the shallow flapping amplitude. Moreover, these mechanisms are particularly well suited to high aspect ratio mosquito wings.
Conflict of interest statement
The authors have no competing financial interests.
Figures
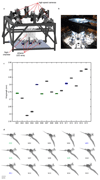






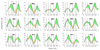

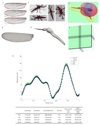
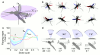



Comment in
-
Biomechanics: The aerodynamics buzz from mosquitoes.Nature. 2017 Apr 6;544(7648):40-41. doi: 10.1038/nature21904. Epub 2017 Mar 29. Nature. 2017. PMID: 28382986 No abstract available.
References
-
- Ellington CP, van den Berg C, Willmott AP, Thomas ALR. Leading-edge vortices in insect flight. Nature. 1996;384:626–630.
-
- Somps C, Luttges M. Dragonfly Flight - Novel Uses of Unsteady Separated Flows. Science. 1985;228:1326–1329. - PubMed
-
- Bomphrey RJ, Srygley RB, Taylor GK, Nudds RL, Thomas ALR. Visualising the flow around insect wings. Phys Fluids. 2002;14:S4.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

