Mechanisms of stochastic onset and termination of atrial fibrillation studied with a cellular automaton model
- PMID: 28356539
- PMCID: PMC5378131
- DOI: 10.1098/rsif.2016.0968
Mechanisms of stochastic onset and termination of atrial fibrillation studied with a cellular automaton model
Abstract
Mathematical models of cardiac electrical excitation are increasingly complex, with multiscale models seeking to represent and bridge physiological behaviours across temporal and spatial scales. The increasing complexity of these models makes it computationally expensive to both evaluate long term (more than 60 s) behaviour and determine sensitivity of model outputs to inputs. This is particularly relevant in models of atrial fibrillation (AF), where individual episodes last from seconds to days, and interepisode waiting times can be minutes to months. Potential mechanisms of transition between sinus rhythm and AF have been identified but are not well understood, and it is difficult to simulate AF for long periods of time using state-of-the-art models. In this study, we implemented a Moe-type cellular automaton on a novel, topologically equivalent surface geometry of the left atrium. We used the model to simulate stochastic initiation and spontaneous termination of AF, arising from bursts of spontaneous activation near pulmonary veins. The simplified representation of atrial electrical activity reduced computational cost, and so permitted us to investigate AF mechanisms in a probabilistic setting. We computed large numbers (approx. 105) of sample paths of the model, to infer stochastic initiation and termination rates of AF episodes using different model parameters. By generating statistical distributions of model outputs, we demonstrated how to propagate uncertainties of inputs within our microscopic level model up to a macroscopic level. Lastly, we investigated spontaneous termination in the model and found a complex dependence on its past AF trajectory, the mechanism of which merits future investigation.
Keywords: atrial fibrillation; cellular automata; model; re-entry; termination.
© 2017 The Authors.
Figures



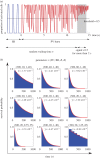
 . Note that when we varied BR, the cumulative distribution was monotonically decreasing for any given time. This indicates that the second classifier identifies the transition rate to enter AF is a monotonic increasing function of BR, in contrast to figure 3 where AF is mostly induced at the intermediate regime of BR.
. Note that when we varied BR, the cumulative distribution was monotonically decreasing for any given time. This indicates that the second classifier identifies the transition rate to enter AF is a monotonic increasing function of BR, in contrast to figure 3 where AF is mostly induced at the intermediate regime of BR.


References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

