Analysis of a Compartmental Model of Endogenous Immunoglobulin G Metabolism with Application to Multiple Myeloma

Abstract

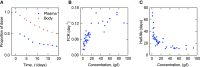
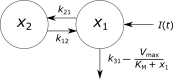
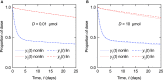
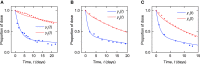
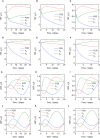
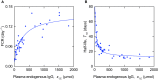
Immunoglobulin G (IgG) metabolism has received much attention in the literature for two reasons: (i) IgG homeostasis is regulated by the neonatal Fc receptor (FcRn), by a pH-dependent and saturable recycling process, which presents an interesting biological system; (ii) the IgG-FcRn interaction may be exploitable as a means for extending the plasma half-life of therapeutic monoclonal antibodies, which are primarily IgG-based. A less-studied problem is the importance of endogenous IgG metabolism in IgG multiple myeloma. In multiple myeloma, quantification of serum monoclonal immunoglobulin plays an important role in diagnosis, monitoring and response assessment. In order to investigate the dynamics of IgG in this setting, a mathematical model characterizing the metabolism of endogenous IgG in humans is required. A number of authors have proposed a two-compartment nonlinear model of IgG metabolism in which saturable recycling is described using Michaelis-Menten kinetics; however it may be difficult to estimate the model parameters from the limited experimental data that are available. The purpose of this study is to analyse the model alongside the available data from experiments in humans and estimate the model parameters. In order to achieve this aim we linearize the model and use several methods of model and parameter validation: stability analysis, structural identifiability analysis, and sensitivity analysis based on traditional sensitivity functions and generalized sensitivity functions. We find that all model parameters are identifiable, structurally and taking into account parameter correlations, when several types of model output are used for parameter estimation. Based on these analyses we estimate parameter values from the limited available data and compare them with previously published parameter values. Finally we show how the model can be applied in future studies of treatment effectiveness in IgG multiple myeloma with simulations of serum monoclonal IgG responses during treatment.

Keywords: biomedical systems; identifiability; immunoglobulin G; lumped-parameter systems; metabolism; multiple myeloma; parameter identification; sensitivity analysis.

Figure 1

(A) Proportion of administered IgG remaining in plasma (blue circles) and the body (red triangles) in a typical normal subject; data from Solomon et al. (1963). Plasma concentration dependence of (B) fractional catabolic rate (FCR) and (C) half-life (T_½) of IgG; redrawn from Waldmann and Strober (1969) with permission from S. Karger AG, Basel.

Figure 2

Endogenous IgG metabolism model schematic.

Figure 3

Simulations of timecourse responses y₁(t) and y₂(t) as described by Equations (5–7) (nonlinear model – solid line) and Equations (8–10) (linearized model – dashed line). The quantity of endogenous IgG in plasma at t = 0, x_1,E(0), is 5 µmol. The tracer dose D is (A) 0.01 µmol and (B) 10 µmol.

Figure 4

Timecourse fits: model described by Equations (8–10) fitted to timecourse data extracted from plots in Solomon et al. (1963) for (A–C) subjects A, B, and C.

Figure 5

Parameter estimates for individual timecourses. Dashed lines connect the estimates obtained for an individual subject.

Figure 6

Traditional sensitivity functions (TSFs) of timecourse outputs y₁(t), for (A–C) subjects A, B and C, and y₂(t), for (D–F) subjects A, B, and C. Generalized sensitivity functions (GSFs) of timecourse outputs y₁(t), for (G–I) subjects A, B, and C, and y₂(t), for (J–L) subjects A, B, and C.

Figure 7

Expressions for (A) FCR (Equation 11) and (B) T_½ (Equation 14) fitted to data from Waldmann and Strober (1969).

Figure 8

Traditional sensitivity functions (TSFs) of (A) FCR and (B) T_½ and generalized sensitivity functions (GSFs) of (C) FCR with respect to model parameters.

Figure 9

Simulations of plasma monoclonal IgG responses in IgG myeloma alongside data from six IgG myeloma patients (A–F).