The evolution of postpairing male mate choice
- PMID: 28369908
- PMCID: PMC5518233
- DOI: 10.1111/evo.13241
The evolution of postpairing male mate choice
Abstract
An increasing number of empirical studies in animals have demonstrated male mate choice. However, little is known about the evolution of postpairing male choice, specifically which occurs by differential allocation of male parental care in response to female signals. We use a population genetic model to examine whether such postpairing male mate choice can evolve when males face a trade-off between parental care and extra-pair copulations (EPCs). Specifically, we assume that males allocate more effort to providing parental care when mated to preferred (signaling) females, but they are then unable to allocate additional effort to seek EPCs. We find that both male preference and female signaling can evolve in this situation, under certain conditions. First, this evolution requires a relatively large difference in parental investment between males mated to preferred versus nonpreferred females. Second, whether male choice and female signaling alleles become fixed in a population versus cycle in their frequencies depends on the additional fecundity benefits from EPCs that are gained by choosy males. Third, less costly female signals enable both signaling and choice alleles to evolve under more relaxed conditions. Our results also provide a new insight into the evolution of sexual conflict over parental care.
Keywords: Extra-pair copulation; female sexual signal; male mate choice; parental care; postpairing.
© 2017 The Author(s). Evolution published by Wiley Periodicals, Inc. on behalf of The Society for the Study of Evolution.
Figures

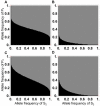


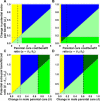

References
-
- Amundsen, T. 2000. Why are female birds ornamented? Trends Ecol. Evol. 15:149–155. - PubMed
-
- Andersson, M.B. 1994. Sexual selection. Princeton Univ. Press, Princeton, NJ.
-
- Barry, K. L. , and Kokko H.. 2010. Male mate choice: why sequential choice can make its evolution difficult. Anim. Behav. 80:163–169.
-
- Berzins L. L., and Dawson R. D.. 2016. Experimentally altered plumage brightness of female tree swallows: a test of the differential allocation hypothesis. Behaviour 153:525–550.
MeSH terms
Associated data
LinkOut - more resources
Full Text Sources
Other Literature Sources
