Risk-based management of invading plant disease

Abstract

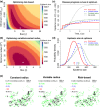
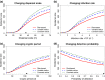
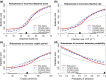
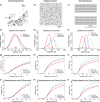
Effective control of plant disease remains a key challenge. Eradication attempts often involve removal of host plants within a certain radius of detection, targeting asymptomatic infection. Here we develop and test potentially more effective, epidemiologically motivated, control strategies, using a mathematical model previously fitted to the spread of citrus canker in Florida. We test risk-based control, which preferentially removes hosts expected to cause a high number of infections in the remaining host population. Removals then depend on past patterns of pathogen spread and host removal, which might be nontransparent to affected stakeholders. This motivates a variable radius strategy, which approximates risk-based control via removal radii that vary by location, but which are fixed in advance of any epidemic. Risk-based control outperforms variable radius control, which in turn outperforms constant radius removal. This result is robust to changes in disease spread parameters and initial patterns of susceptible host plants. However, efficiency degrades if epidemiological parameters are incorrectly characterised. Risk-based control including additional epidemiology can be used to improve disease management, but it requires good prior knowledge for optimal performance. This focuses attention on gaining maximal information from past epidemics, on understanding model transferability between locations and on adaptive management strategies that change over time.

Keywords: adaptive control; citrus canker; disease management; eradication; risk-based control; stakeholders; stochastic epidemic model.

Figure 1

The model and its default behaviour when there is no control. (a) The underlying epidemiological model. Host plants move from susceptible (S) to cryptic (C) when first infected; from C to infected (I) as symptoms emerge; and can be removed (R) due to control after being detected via a survey. (b) Typical epidemic when there is no control. (c) Disease progress curve when there is no control. Shades of blue show the deciles of the distribution; black curve shows the median.

Figure 2

Risk‐based control outperforms variable radius control, which outperforms constant radius control. (a) Optimising the risk‐based strategy; the optimised threshold and bias parameters, which lead to the smallest average epidemic size (i.e. number of hosts removed by the end of the epidemic when the pathogen is eradicated), are E _min = 0.00075 and $\mathrm{\gamma }$ = 8.2, respectively (marked with a white circle). (b) Optimising the variable radius strategy: the optimal values R* = 6 m and $\mathrm{\gamma }$ = 2.45 are marked with a white circle. The optimal constant radius strategy can be identified from this plot by considering only values of R* with $\mathrm{\gamma }$ = 0 (cf. Eqns 10, 11); this value, R* = 31 m, is marked with a white square. (c) Disease progress curves at the optima identified in (a) and (b), showing the mean of 5000 simulation runs for each strategy for each time. (d) Probability distributions of the final epidemic size for each strategy using the optimised parameters, showing the variability in the eventual total number of removals. The mean epidemic sizes are marked by the letters just above the x‐axis. (e) State at the end of a randomly chosen epidemic with control for each control strategy. The black circles show the removal radii around particular hosts; crosses denote a removal radius of zero. Full time‐courses of these particular (indicative) epidemics are given in Supporting Information Videos [Link], [Link], [Link].

Figure 3

The relative performance of the control strategies does not depend on values of epidemiological and management parameters (when they are known in advance of the epidemic). (a) Response of the optimal performance of the three control strategies to the dispersal scale, independently optimising the performance of each strategy at each value of the dispersal parameter (i.e. repeating the process underlying Fig. 2(a,b) for each dispersal scale, $\mathrm{\alpha }$). The mean epidemic size (i.e. mean number of hosts removed by the time of eradication) at optimum is shown on the y‐axis of the graph, and the default dispersal scale is marked by the black triangle on the x‐axis. (b) As for (a), but showing response to the rate of secondary infection, $\mathrm{\beta }$. (c) As for (a), but showing response to the average cryptic period, $1/\mathrm{\sigma }$. (d) As for (a), but showing response to the probability of detecting symptomatic hosts in a single round of surveying, p _d.

Figure 4

Performance of the risk‐based and variable radius control strategies degrades if parameters are not known in advance of the epidemic. (a) Response of the performance of the three control strategies to changes in the dispersal scale, when the control strategies were optimised incorrectly using the default dispersal scale, and when this default scale is used during the epidemic to calculate $E_{i,n}^{\mathrm{eff}}$ (Eqn 7 and $R_i^{max}$ (Eqn 10). The average epidemic size (i.e. mean number of hosts removed by the time of eradication) for the risk‐based strategy when optimised correctly is shown for comparison (dash‐dotted line). The mean epidemic size is shown on the y‐axis of the graph, and the default dispersal scale is marked by the black triangle on the x‐axis. The range of dispersal scales for which the (incorrectly optimised) risk‐based strategy outperforms the (incorrectly optimised) variable radius strategy is marked by the grey shading along the x‐axis. The range for which the risk‐based strategy outperforms the (incorrectly optimised) constant radius strategy but is outperformed by the (incorrectly optimised) variable radius strategy is shown by the black shading. (b) As for (a), but for misspecification of the rate of secondary infection. (c) As for (a), but for misspecification of the average cryptic period. (d) As for (a), but for misspecification of the probability of detecting symptomatic hosts.

Figure 5

The relative performance of the control strategies does not depend on host landscape structure, but the improvement from risk‐based control is smaller when dispersal is thin‐tailed. (a–c) Host landscapes and dispersal kernel combinations used to assess the robustness of the methods: Miami Broward County Site B2 using an exponential dispersal kernel; a random landscape consisting of 2000 hosts randomly positioned over 1 km² (with Cauchy dispersal); and a small citrus orchard, consisting of 2016 hosts at a regular spacing (with Cauchy dispersal). (d–f) Full probability distributions of the epidemic sizes at optimum. Mean epidemic size (i.e. mean number of hosts removed by the time of eradication) for each strategy is marked by letters just above the x‐axis of each plot. (g–i) Responses of average epidemic size at optimum to changes in the rate of secondary infection. The default rate of secondary infection is marked with a triangle on the x‐axis of each plot. (j–l) Responses of average epidemic size at optimum to changes in the scale parameter of the dispersal kernel. Again the default value is marked with a triangle.