On the buckling of elastic rings by external confinement

Abstract

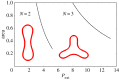
We report the results of an experimental and numerical investigation into the buckling of thin elastic rings confined within containers of circular or regular polygonal cross section. The rings float on the surface of water held in the container and controlled removal of the fluid increases the confinement of the ring. The increased compressive forces can cause the ring to buckle into a variety of shapes. For the circular container, finite perturbations are required to induce buckling, whereas in polygonal containers the buckling occurs through a linear instability that is closely related to the canonical Euler column buckling. A model based on Kirchhoff-Love beam theory is developed and solved numerically, showing good agreement with the experiments and revealing that in polygons increasing the number of sides means that buckling occurs at reduced levels of confinement.This article is part of the themed issue 'Patterning through instabilities in complex media: theory and applications.'

Keywords: buckling; confined; ring.

Figure 1.

Buckling modes of a thin-walled elastic ring under uniform transmural pressure, P_ext, scaled by Eh³/(12R³(1−ν²)), quantified by enclosed area scaled by πR². A series of symmetry-breaking bifurcations is present, with each bifurcation corresponding to a different azimuthal mode number, N. The most unstable mode is N=2, which is typically seen in experiments. These post-buckling curves are computed via finite-element solution of equation (2.1) under increasing constant external pressure load. (Online version in colour.)

Figure 2.

Schematic of the experimental set-up: an elastic ring floats on the surface of water confined within a funnel of given cross-section. (Online version in colour.)

Figure 3.

Overhead images from experiments and computations (using the penalty pressure formulation) in triangular, square and pentagonal containers for buckled shapes that maintain the discrete symmetry of the polygon. Note that the symmetry is approximate in the experimental images. (Online version in colour.)

Figure 4.

Compression in a conical funnel with circular cross section. Experimental data for buckled state are shown as black markers. Simulation results for the penalty pressure formulation are shown for the trivial branch (dotted black line) and the buckled solution (solid black line). The dashed red line shows results using the Euler–Bernoulli beam model developed by Chan & McMinn [13]. The buckled solutions from the Chan & McMinn model are shown for a fluid area of 3868 mm². The unstable solution contains a small region of buckling, whereas the stable solution has a significant buckle. An experimental image for a fluid area of 3756 mm² is also shown. (Online version in colour.)

Figure 5.

Comparison of experimental data (markers) on the main (full-symmetry) branch (black triangles) and after finite perturbation (smaller red triangles) against model predictions (solid lines) for the main branch (black, upper line) and a two-lobed post-buckling branch (red, lower line) in a square funnel. Simulation results are shown on the main branch for: (a) unbuckled state at fluid area of3675 mm²; the right-hand side corresponds to the penalty pressure approach and the left-hand side corresponds to exact contact; and (b) buckled mode with full symmetry at a fluid area of 1654 mm². On the finite perturbation branch, (c)–(e) correspond to buckled states with single reflection symmetry at the same fluid area of 3443 mm². An experimental image is shown on the finite perturbation branch (f) corresponding to a fluid area of 3430 mm². (Online version in colour.)

Figure 6.

Critical buckling radius of the inscribed circle for a regular n-gon relative to the undeformed radius of the ring (r_crit/R) for an inextensible Euler–Bernoulli model (large black triangles) and the Kirchhoff–Love model (small red dots). The asymptotic approximation, equation(3.6), for the critical load in the Euler–Bernoulii model is shown as a dotted line. Inset: Sketch of geometry for Euler–Bernoulli model. Equation (3.1) is solved between two regions of flat contact, subject to an overall length constraint. Contact forces are determined as part of the solution. (Online version in colour.)